Tại sao một quả lắc đồng hồ có thể đung đưa liên tục trong nhiều ngày mà không cần cung cấp thêm năng lượng? Câu trả lời sẽ được giải đáp khi chúng ta tìm hiểu về cơ năng trong dao động điều hòa ngay sau đây.
Cơ năng
– Trong dao động điều hòa, có sự chuyển hóa qua lại giữa động năng và thế năng của vật, nhưng cơ năng (tổng động năng và thế năng) được bảo toàn.
W=Wt+Wd=Wmax=12mω2A2
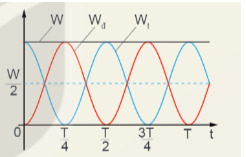
Cơ năng của con lắc đơn và con lắc lò xo
Cơ năng của con lắc lò xo
Con lắc lò xo:
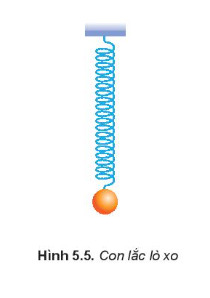
Con lắc lò xo trong giao động điều hòa
– Nếu bỏ qua ma sát, dao động của con lắc lò xo là dao động điều hòa.
– Thế năng của con lắc lò xo:
Wt=12kx2
với k là độ cứng của lò xo.
– Cơ năng của con lắc lò xo:
W=Wt+Wd=12kx2+12mv2=12mω2A2=12kA2
– Tần số góc:
ω=√km
– Chu kỳ:
T=2π√mk
Xem thêm: >> Gia tốc của dao động điều hòa <<
Cơ năng của con lắc đơn
Con lắc đơn:
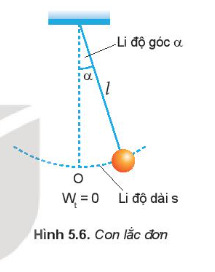
Con lắc đơn trong giao động điều hòa
– Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc α.
– Thế năng của con lắc đơn là thế năng trọng trường.
Chọn mốc thế năng ở vị trí cân bằng, thế năng của con lắc tại li độ góc α là:
Wt=mgl(1–cosα)
– Khi α nhỏ thì
sinα2≈α2 (α được tính theo rad).
– Khi đó:
Wt=mglα22=12mgls2vớiα=sl
Bài viết đã trình bày chi tiết các công thức tính cơ năng của con lắc lò xo và con lắc đơn. Hiểu rõ về cơ năng sẽ giúp chúng ta giải thích nhiều hiện tượng vật lý trong cuộc sống và câu hỏi từ đầu đã đưa ra.










 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa