Phương trình mặt cầu và các dạng bài tập thường gặp | Toán 12

Phương trình mặt cầu viết thế nào? Mỗi dạng bài sẽ có phương pháp giải riêng biệt để tìm ra phương trình mặt cầu chuẩn xác. Đây là một chuyên đề khó trong chương trình toán 12 và không phải học sinh nào cũng có thể học tốt và giải đúng. Hiểu được điều này, kienthucthpt sẽ cung cấp kiến thức lý thuyết phương trình mặt cầu, kèm thêm các dạng bài tập và cách giải chi tiết để các em tham khảo.

Mặt cầu là gì?

Trước khi tìm hiểu về phương trình mặt cầu trong không gian, đầu tiên các em cần nắm vững định nghĩa của mặt cầu. Theo chương trình hình học THPT, mặt cầu được định nghĩa là tập hợp các điểm nằm cách đều một điểm cố định một khoảng không đổi, gọi là bán kính. Điểm cố định này được gọi là tâm mặt cầu.

Tìm hiểu Mặt cầu là gì?

Ngoài ra, mặt cầu còn có thể được định nghĩa theo mặt tròn xoay. Trong trường hợp này, mặt cầu chính là hình tròn xoay tạo ra khi quay một đường tròn quanh một đường kính của nó.

Phương trình mặt cầu là gì?

Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là:

(S): (x – a)² + (y – b)² + (z – c)² = R² (1)

Phương trình mặt cầu nói trên có thể viết dưới dạng:

(S) : x² + y² + z² + 2ax + 2by + 2cz + d = 0 (2) với d = a² + b² + c² – R2

Từ đó ta có phương trình (2) với điều kiện a² + b² + c² – d > 0 là phương trình mặt cầu tâm I (-a; -b; -c) có bán kính là:

Đặc biệt nếu mặt cầu (S) có tâm O (0;0;0) và bán kính R thì phương trình mặt cầu (S) là:

(S): x² + y² + z² = R²

>> Xem thêm: Lý thuyết Nguyên hàm

Cách viết phương trình mặt cầu dễ hiểu nhất

Cho phương trình mặt cầu:

$(S): (x – a)^2 + (y – b)^2 + (z – c)^2 = R$

với tâm I(a; b; c) và bán kính R.

$(S): x^2 + y^2 + z^2 – 2ax – 2by – 2cz + d = 0$

với tâm I(a; b; c)

$R = \sqrt{a^2 + b^2 + c^2 – d}$

Ta có công thức tính khoảng cách từ tâm mặt cầu đến mặt phẳng để xét vị trí tương đối giữa mặt phẳng và mặt cầu:

$d(I, (P)) = \frac{|A.a + B.b + C.c + D|}{\sqrt{A^2 + B^2 + C^2}}$

>> Xem thêm: Xác xuất có điều kiện

Một số bài tập phương trình mặt cầu lớp 12 thường gặp

Xem chi tiết bài tập về phương trình mặt cầu tại đây:

Gợi ý một số bài tập cơ bản học sinh cần nắm:

Bài tâp 1: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x – 1)² + (y – 2)² + (z – 1)² = 9. Tính tọa độ tâm I và bán kính R của (S).

Hướng dẫn giải

Dựa vào phương trình mặt cầu (S): (x – 1)² + (y – 2)² + (z – 1)² = 9 , ta có tâm I(-1;2;1) và

Bài tập 2: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x² + y² + z² + 2x – 4y + 6z – 2 = 0. Tính tọa độ tâm I và bán kính R của (S).

Hướng dẫn giải

Dựa vào phương trình mặt cầu x² + y² + z² + 2x – 4y + 6z – 2 = 0, ta có:

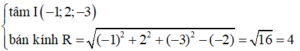
Bài tập 3: Cho phương trình (S):x² + y² + z² + 2(3 – m)x – 2(m + 1)y – 2mz + 2m2 + 7 = 0. Tìm tất cả giá trị của m để (S) là một phương trình mặt cầu.

Hướng dẫn giải

Gọi tâm của mặt cầu là I (a ; b ; c) và bán kính là R.

Ta có : a = m – 3, b = m + 1, c = m, d = 2m2 + 7.

(S) là mặt cầu <=> a² + b² + c² – d > 0 

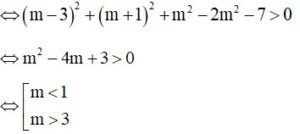
Bài tập 4: Trong không gian Oxyz cho điểm A (–1; 2; 0), viết phương trình mặt cầu tâm A bán kính bằng 4

Hướng dẫn giải

Dạng phương trình mặt cầu (S) : (x – a)² + (y – b)² + (z – c)² = R2

Tâm là A suy ra a = –1, b = 2, c = 0 và R = 4

Thế vào phương trình mặt cầu (S) ta được  (S):  (x + 1)² + (y – 2)² + z² = 16