Vectơ trong không gian lớp 12 luôn là một dạng toán khó, đòi hỏi các em phải hiểu sâu và nắm vững kiến thức mới có thể hiểu bài và đạt được điểm cao. Để thực sự hiểu rõ kiến thức về dạng toán này, hãy cùng kienthucthpt tìm hiểu kỹ hơn nhé!
Lý thuyết vectơ trong không gian

Vectơ trong không gian là gì?
– Vectơ trong không gian là một đoạn thẳng có hướng.
– Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Tương tự như vectơ trong mặt phẳng, đối với vectơ trong không gian, ta cũng có các ký hiệu và khái niệm sau:
– Vectơ có điểm đầu là A và điểm cuối là B được ký hiệu là →AB.
– Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ thì vectơ còn được ký hiệu là →a, →b, →x, →y….
– Độ dài của vectơ →AB được ký hiệu là |\overrightarrow{AB}|, độ dài của vectơ →a được ký hiệu là | →a |.
– Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Hai vectơ cùng phương, cùng hướng, ngược hướng và hai vectơ bằng nhau
– Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
– Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
– Hai vectơ →a và →b được gọi là bằng nhau, ký hiệu →a = b, nếu chúng có cùng độ dài và cùng hướng.
Chú ý: Tương tự như vectơ trong mặt phẳng, ta có tính chất và các quy ước sau đối với vectơ trong không gian:
– Trong không gian, với mỗi điểm O và vectơ →a cho trước, có duy nhất điểm M sao cho →OM=→a
– Các vectơ có điểm đầu và điểm cuối trùng nhau, ví dụ như →AA, →BB gọi là các vectơ-không.
– Ta quy ước vectơ-không có độ dài là 0, cùng hướng (và vì vậy cùng phương) với mọi vectơ. Do đó, các vectơ-không đều bằng nhau và được ký hiệu chung là →0.
Tổng và hiệu của hai vectơ trong không gian
Tổng của hai vectơ trong không gian
– Trong không gian, cho hai vectơ →a và →b. Lấy một điểm A bất kỳ và các điểm B, C sao cho →AB=→a; →BC=→b
Khi đó, vectơ →AC được gọi là tổng của hai vectơ →a và →b, ký hiệu là →a+→b
– Trong không gian, phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
Nhận xét: Quy tắc ba điểm và quy tắc hình bình hành trong mặt phẳng vẫn đúng trong không gian:
- Nếu A, B, C là ba điểm bất kỳ thì →AB+→BC=→AC
- Nếu ABCD là hình bình hành thì →AB+→AD=→AC
Vectơ đối
Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ →a, a được gọi là vectơ đối của vectơ →a, ký hiệu là – →a
Chú ý:
- Hai vectơ là đối nhau nếu và chỉ nếu tổng của chúng bằng →0
- Vectơ →BA là một vectơ đối của vectơ →AB
- Vectơ →0 được coi là vectơ đối của chính nó.
Hiệu của hai vectơ trong không gian
Vectơ →a+(−→b) được gọi là hiệu của hai vectơ →a và →b và ký hiệu là →AB–→a
Trong không gian, phép lấy hiệu của hai vectơ được gọi là phép trừ vectơ.
Nhận xét: Với ba điểm O, A, B bất kỳ trong không gian, ta có: →OB–→OA=→AB
Tích của một số với một vectơ trong không gian
Trong không gian, tích của một số thực k ≠ 0 với một vectơ →a≠→0 là một vectơ, ký hiệu là k→a, được xác định như sau:
- Cùng hướng với vectơ →a nếu k > 0; Ngược hướng với vectơ →a nếu k < 0
- Có độ dài bằng |k|⋅|→a|
Trong không gian, phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ.
Chú ý:
- Quy ước →a=→0 nếu k = 0 hoặc →a=→0
- Nếu k→a=→0 thì k = 0 hoặc →a=→0
- Trong không gian, điều kiện cần và đủ để hai vectơ →a và →b (→b ≠ 0 cùng phương là có một số thực k sao cho →a = k→b
Tích vô hướng của hai vectơ trong không gian
Góc giữa hai vectơ trong không gian
Trong không gian, cho hai vectơ →a và →b khác →0
Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho →OA=→a, →OB = →b
Khi đó, góc
^AOB (0∘≤^AOB≤180∘)được gọi là góc giữa hai vectơ →a và →b , ký hiệu là (→a,→b)
Chú ý:
- Để xác định góc giữa hai vectơ →AB và →CD
trong không gian, ta có thể lấy điểm E sao cho →AE=→CD , khi đó →AB,(−→CD) = ∠BAE
- Quy ước góc giữa một vectơ bất kỳ và →0 có thể nhận một giá trị tùy ý từ
0∘đến
180∘.
Tích vô hướng của hai vectơ trong không gian
Trong không gian, cho hai vectơ →a và →b đều khác →0
Tích vô hướng của hai vectơ →avà →b là một số, ký hiệu là →a. →b, được xác định bởi công thức:
→a⋅→b=|→a|⋅|→b|⋅cos(∠(→a,→b))
Chú ý:
- Quy ước nếu →a = →0 hoặc →b = →0 thì →a.→b = 0
- Cho hai vectơ →a, →b đều khác →0
Khi đó: →a ⊥ →b ⟺ →a . →a = 0
- Với mọi vectơ →a, ta có: →a2=|→a|2
- Nếu →aa, →ab là hai vecto khác →0 thì
cos(→a,→b)=→a⋅→b∣→a∣⋅∣→b∣
>> Xem thêm: Tính đơn điệu của hàm số
Bài tập về vectơ trong không gian

Bài tập 1:
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Biết AB = 1, BC = 2, AA’ = 3
a) Hãy kể tên các vectơ có điểm đầu là A và điểm cuối là một trong các đỉnh còn lại của hình hộp chữ nhật.
b) Trong các vectơ →BC, →BA, →BB, →BA′, hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)
c) Tính độ dài các vectơ →AB, →BC, →AA′
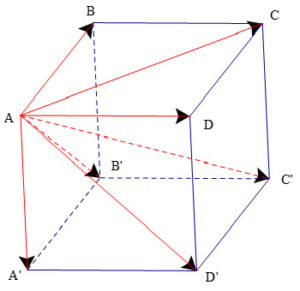
Giải:
a) →AB, →AC, →AD, →AA′, →AB′, →AC′, →AD′
b) Trong các vectơ →BC, →BA, →BB′, →BA′, hai vectơ →BC và →BA có giá cùng nằm trong mặt phẳng (ABCD).
c) |→AB|=1,|→BC|=2,|→AA′|=3.
Bài tập 2: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 1. BC = 2. Tính độ dài của vectơ →A′B′ + →BC.
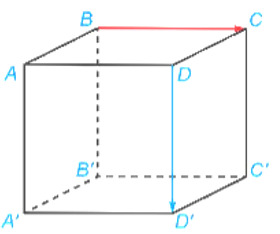
Giải:
Vì tứ giác ABB’A’ là hình chữ nhật nên →AB = →A′B′
Do đó, →A′B′ + →BC = →AB + →BC = →AC
Vì ABCD là hình chữ nhật nên
AC=√AB2+BC2=√1+4=√5Suy ra |→A′B+→BC|=√5
>> Xem thêm: Phương trình mặt cầu
Bài tập 3: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác AB’C. Chứng minh →BD′ = 3→BG
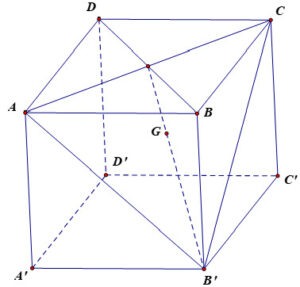
Giải:
Áp dụng quy tắc hình hộp ta có:
→BD′=→BA+→BC+→BB′(1).
Vì G là trọng tâm của tam giác AB’C nên
→BA+→BC+→BB′=3→BG(2).
Từ (1) và (2) suy ra
→BD′=3→BG.Trên đây là toàn bộ kiến thức về vectơ trong không gian thuộc chương trình Toán lớp 12 mà chúng tôi đã nghiên cứu và tổng hợp. Hy vọng rằng, sau bài viết này, các em đã có thể nắm vững kiến thức về dạng bài vectơ trong không gian và luyện tập một cách thuần thục. Để có thêm các thông tin bổ ích, các em hãy truy cập Toán 12 mỗi ngày nhé!
















 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa