Tóm tắt lý thuyết Toán 10 Bài 9 Tích của một vectơ với một số theo sách Kết nối tri thức, được trình bày chi tiết và hay nhất sẽ giúp các em học sinh nắm vững kiến thức trọng tâm và ôn luyện hiệu quả để học tốt môn Toán 10.
Tích của một vectơ với một số trong Toán 10
Tích của một vectơ →a≠→0 với một số thực k > 0 là một vectơ, kí hiệu là k →a , cùng hướng với vectơ →a và có độ dài bằng k→a
Ví dụ: Cho hình vẽ sau:
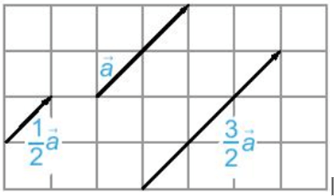
– Vectơ 12→a cùng hướng với vectơ →avà (12→a)=12‖→a‖
– Vectơ 32→a cùng hướng với vectơ →avà (32→a)=32‖→a‖
- Tích của một vectơ →a≠→0với một số thực k < 0 là một vectơ, kí hiệu là k→a, ngược hướng với vectơ →a và có độ dài bằng (–k) |→a|
Chú ý: Ta quy ước k→a = →0 nếu →a = →0 hoặc k=0
Nhận xét: Vectơ k→a có độ dài bằng |k||→a| và cùng hướng với →a nếu k ≥ 0, ngược hướng với →a nếu →a≠→0
Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số
Tìm hiểu các tính chất của phép nhân vectơ với một số
Với hai vectơ →a, →b và hai số thực k, t, ta luôn có :
+) k(t→a)=(kt)→a;
+) k(→a+→b)=k→a+k→b;k(→a–→b)=k→a–k→b;
+) (k+t)→a=k→a+t→a;
+) 1→a=→a;(−1)→a=−→a.
Nhận xét:
Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi →IA+→IB=→0
Điểm G là trọng tâm của tam giác ABC khi và chỉ khi →GA+→GB+→GC=→0
Ví dụ : Cho tam giác ABC. Hãy xác định điểm M để →MA+3→MB+2→MC=→0
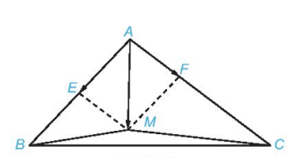
Để xác định vị trí của M, trước hết ta biểu thị →AM (với gốc A đã biết) theo hai vectơ đã biết →AB, →AC
→MA+3→MB+2→MC=→0
⇔→MA+3(→MA+→AB)+2(→MA+→AC)=→0
⇔6→MA+3→AB+2→AC=→0
⇔→AM=12→AB+13→AC
Lấy điểm E là trung điểm của AB và điểm F thuộc cạnh AC sao cho AF=13AC
Khi đó →AE=12→ABvà→AF=13→AC. Vì vậy →AM=→AE+→AF
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.
Qua bài viết này, đã giúp các em hiểu rõ hơn lý thuyết về tích của một vectơ với một số và cách thực hiện phép toán này. Hy vọng rằng kiến thức này sẽ hỗ trợ các trong học tập và giúp các em giải quyết các bài toán phức tạp hơn trong những bài học sắp tới
<<Xem thêm>> Lý thuyết Bài 5 Toán 10: Giá trị lượng giác của một góc










 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa