Các số đặc trưng đo xu thế trung tâm | Kết nối tri thức

Tóm tắt lý thuyết Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm sách Kết nối tri thức chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Số trung bình và trung vị

Số trung bình

Cho mẫu số liệu $x_1, x_2, x_3, \dots, x_n$

– Số trung bình (hay TB cộng) của mẫu số liệu, kí hiệu là $\bar{x}$, được tính bằng công thức:
$$\bar{x} = \frac{x_1 + x_2 + x_3 + \dots + x_n}{n}$$

– Đối với mẫu số liệu cho dưới dạng bảng tần số, số trung bình được tính như sau:
$$\bar{x} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3 + \dots + m_k x_k}{n}$$
Với $m_i$ là tần số của giá trị $x_i$ và $n = m_1 + m_2 + \dots + m_k$.

⇒ Ý nghĩa: Số trung bình là giá trị trung bình cộng, cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.

Trung vị

– Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), ta dùng trung vị để đo xu thế trung tâm.

Ví dụ: Mẫu số liệu: 1, 3, 2, 3, 4, 20

Tìm trung vị:

– Bước 1: Sắp xếp các giá trị theo thứ tự không giảm $X_1, X_2, \dots, X_n$.

– Bước 2: Cỡ mẫu = n.

• Nếu $n$ lẻ ($n = 2k – 1$) thì trung vị là $X_k$.
• Nếu $n$ chẵn ($n = 2k$) thì trung vị bằng $\frac{1}{2}(X_k + X_{k+1})$.

⇒ Ý nghĩa: Trung vị là giá trị ở vị trí chính giữa của mẫu số liệu đã sắp xếp theo thứ tự không giảm. Trung vị không bị ảnh hưởng bởi các giá trị bất thường như số trung bình.

Tứ phân vị

Tứ phân vị gồm 3 giá trị $Q_1, Q_2, Q_3$, chúng chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần đều chứa 25% giá trị.

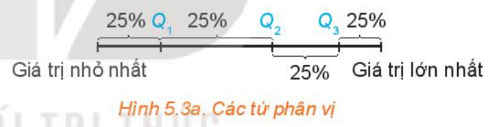
Các bước tìm tứ phân vị:

– Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm.

– Bước 2: Tìm trung vị, chính là $Q_2$.

– Bước 3: $Q_1$ là trung vị của nửa số liệu bên trái $Q_2$ (không bao gồm $Q_2$ nếu $n$ lẻ).

– Bước 4: $Q_3$ là trung vị của nửa số liệu bên phải $Q_2$ (không bao gồm $Q_2$ nếu $n$ lẻ).

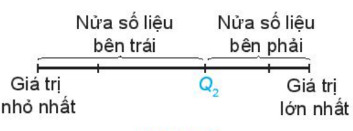
Chú ý:

– $Q_1$ còn được gọi là tứ phân vị thứ nhất hoặc tứ phân vị dưới.

– $Q_3$ còn được gọi là tứ phân vị thứ ba hoặc tứ phân vị trên.

Mốt

– Mốt của một mẫu số liệu là giá trị có tần số xuất hiện nhiều nhất trong mẫu.

– Ý nghĩa: Mốt được sử dụng để xác định xu hướng trung tâm của mẫu số liệu, đặc biệt hữu ích khi mẫu có nhiều giá trị lặp lại.

– Nhận xét:

• Mẫu số liệu có thể có nhiều hơn một mốt nếu có nhiều giá trị xuất hiện với tần số lớn nhất.
• Nếu tất cả các giá trị trong mẫu đều xuất hiện với tần số như nhau, mẫu số liệu đó không có mốt.

>> Xem thêm: Dãy số (Lý thuyết Toán 11) <<

Bài tập Các số đặc trưng đo xu thế trung tâm (Có lời giải)

Bài 1. Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Tuổi thọ (tính theo năm) của 6 loại bóng đèn được ghi lại như sau:

19, 20, 31, 18, 26, 24

b) Số cân nặng (tính theo kg) của 9 học sinh lớp 10D được ghi lại như sau:

37, 37, 40, 42, 45, 40, 42, 42, 55

Hướng dẫn giải:

a) Tuổi thọ trung bình của 6 loại bóng đèn là:
$$\frac{19 + 20 + 31 + 18 + 26 + 24}{6} = 23 \text{ (năm)}$$

– Ta tìm trung vị của mẫu số liệu:

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 20 và 24.

Vậy trung vị của mẫu số liệu là:
$$\frac{20 + 24}{2} = 22$$

– Vì các giá trị 18, 19, 20, 24, 26, 31 trong mẫu số liệu đều xuất hiện với tần số như nhau (1 lần) nên mẫu số liệu này không có mốt.

– Ta tìm tứ phân vị của mẫu số liệu:

Giá trị $Q_2$ chính là trung vị của mẫu số liệu. Do đó ta có $Q_2 = 22$.

– Ta tìm $Q_1$ là trung vị của nửa số liệu bên trái $Q_2$:

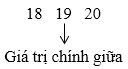
⇒ Giá trị chính giữa lúc này là 19. Ta suy ra $Q_1 = 19$.

– Ta tìm $Q_3$ là trung vị của nửa số liệu bên phải $Q_2$:

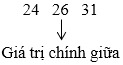
⇒ Giá trị chính giữa lúc này là 26. Ta suy ra $Q_3 = 26$.

Vậy các tứ phân vị của mẫu số liệu là $Q_1 = 19$, $Q_2 = 22$, $Q_3 = 26$.

b) Số cân nặng trung bình của 9 học sinh lớp 10D là:
$$\frac{37 + 37 + 40 + 42 + 45 + 40 + 42 + 42 + 55}{9} \approx 42,22 \text{ (kg)}$$

– Ta tìm trung vị của mẫu số liệu:

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

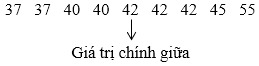
Trung vị của mẫu số liệu là 42.

– Ta thấy giá trị 42 xuất hiện với tần số cao nhất (3 lần) nên mốt của mẫu số liệu này là 42.

– Ta tìm tứ phân vị của mẫu số liệu:

Giá trị $Q_2$ chính là trung vị của mẫu số liệu. Do đó ta có $Q_2 = 42$.

– Ta tìm $Q_1$ là trung vị của nửa số liệu bên trái $Q_2$:

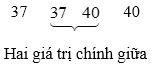
⇒ Dãy trên có hai giá trị chính giữa là 37 và 40. Do đó $Q_1 = \frac{37 + 40}{2} = 38,5$.

– Ta tìm $Q_3$ là trung vị của nửa số liệu bên phải $Q_2$:

⇒ Dãy trên có hai giá trị chính giữa là 42 và 45. Do đó $Q_3 = \frac{42 + 45}{2} = 43,5$.

Vậy các tứ phân vị của mẫu số liệu là $Q_1 = 38,5$, $Q_2 = 42$, $Q_3 = 43,5$.

>> Xem thêm: Mẫu số liệu ghép nhóm Toán 11 << 

Bài 2. Số lượng học sinh giỏi Quốc gia năm học 2019 – 2020 của 10 trường Trung học phổ thông được cho như sau:

0, 0, 9, 0, 0, 4, 0, 0, 0, 6

a) Tìm số trung bình, mốt và các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

Hướng dẫn giải:

a) Số lượng học sinh trung bình là:
$$\frac{0 + 0 + 9 + 0 + 0 + 4 + 0 + 0 + 0 + 6}{10} = 1,9 \text{ (học sinh)}$$

– Ta tìm trung vị của mẫu số liệu:

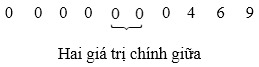
⇒ Dãy trên có hai giá trị chính giữa cùng bằng 0.

Vậy trung vị của mẫu số liệu cũng bằng 0.

– Ta thấy giá trị 0 xuất hiện với tần số cao nhất (7 lần) nên mốt của mẫu số liệu này là 0.

– Ta tìm tứ phân vị của mẫu số liệu:

Giá trị $Q_2$ chính là trung vị của mẫu số liệu. Do đó ta có $Q_2 = 0$.

– Ta tìm $Q_1$ là trung vị của nửa số liệu bên trái $Q_2$:

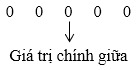
⇒ Giá trị chính giữa lúc này là 0. Ta suy ra $Q_1 = 0$.

– Ta tìm $Q_3$ là trung vị của nửa số liệu bên phải $Q_2$:

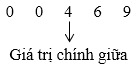
⇒ Giá trị chính giữa lúc này là 4. Ta suy ra $Q_3 = 4$.

Vậy các tứ phân vị của mẫu số liệu là $Q_1 = 0$, $Q_2 = 0$, $Q_3 = 4$.

b) Vì mẫu số liệu tập trung với mật độ cao ở bên trái $Q_2$, tức là trung vị, nên tứ phân vị thứ nhất $Q_1$ và trung vị $Q_2$ trùng nhau.