Trong chương trình học Toán lớp 12, việc tìm giá trị lớn nhất và giá trị nhỏ nhất của một hàm số là một kỹ năng quan trọng mà mỗi học sinh cần nắm vững.
Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách xác định giá trị lớn nhất và giá trị nhỏ nhất của các hàm số, điển hình trong chương trình học, qua đó giúp các em học sinh có thể áp dụng thành thạo vào giải các bài tập liên quan.
Kiến thức THPT sẽ đưa ra các ví dụ minh họa cụ thể, bao gồm cả lý thuyết và bài tập thực hành, để các em có thể hiểu rõ và vận dụng hiệu quả trong quá trình ôn tập và thi cử.
Định nghĩa giá trị lớn nhất giá trị nhỏ nhất lớp 12

Cho hàm số y = f(x) xác định trên tập D
{f(x)≤M,∀x∈D∃x0∈D sao cho f(x0)=M
Ký hiệu: M=maxDf(x)
– Số m là giá trị nhỏ nhất (GTNN) của hàm số f trên D
{f(x)≥m,∀x∈D∃x0∈D sao cho f(x0)=m
Ký hiệu: m=minDf(x)
>> Xem thêm: Phương trình mặt cầu và các dạng bài tập thường gặp | Toán 12
Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Định lí
Nếu một hàm số liên tục trên một khoảng nào đó, thì nó sẽ đạt được giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó.
Quy tắc tìm GTLN, GTNN của hàm số y = f(x) liên tục trên đoạn [a;b]
Tìm các điểm xi∈(a,b)(i=1,2,…,n) mà tại đó f′(xi)=0 hoặc f′(xi) không xác định
Tính f(a),f(b),f(xi)(i=1,2,…,n)
Khi đó: max[a,b]f(x)=max{f(a),f(b),f(xi)
min[a,b]f(x)=min{f(a),f(b),f(xi)
>> Xem thêm: Vectơ trong không gian (Lý thuyết + Bài tập) | Kết nối tri thức
Ví dụ minh họa giá trị lớn nhất giá trị nhỏ nhất lớp 12
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x3 – 3×2 – 9x + 2 trên đoạn [-2; 2]
Hướng dẫn
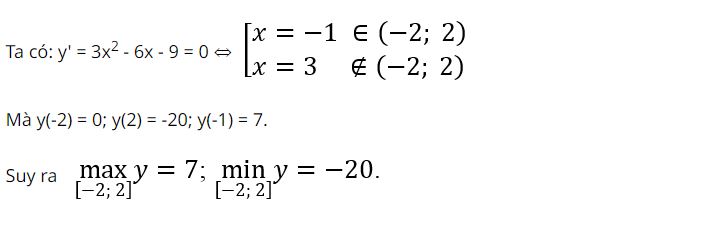
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=x+√4–x2
Hướng dẫn
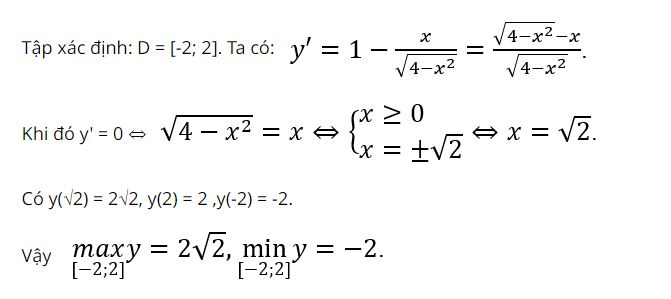











 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa