Lý thuyết Bài 5 Toán 10: Giá trị lượng giác của một góc

Trong toán học, giá trị lượng giác của một góc đóng vai trò thiết yếu trong việc giải quyết các bài toán hình học và đại số. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về các khái niệm và công thức liên quan với cách trình bày ngắn gọn dễ hiểu.

Tìm hiểu giá trị lượng giác của một góc

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

Cho trước một góc α, \(0^\circ \leq \alpha \leq 180^\circ\). Khi đó, có duy nhất điểm M(\(x_0\); \(y_0\)) trên nửa đường tròn đơn vị để .

– Định nghĩa tỉ số lượng giác của một góc từ \(0^\circ\)đến \(180^\circ\)

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho \(\widehat{xOM} = \alpha\). Khi đó:

+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là \(\frac{y_0}{x_0}\), được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là \(\frac{x_0}{y_0}\), được kí hiệu là cot α.

– Từ định nghĩa trên ta có:

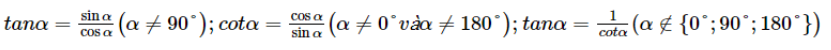
– Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

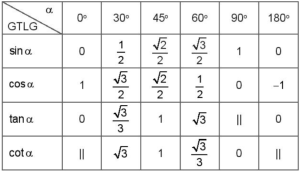
Bảng giá trị lượng giác

Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Ví dụ: Tìm các giá trị lượng giác của góc 120°

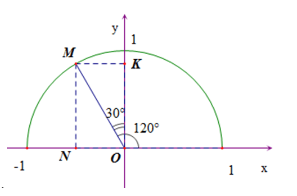
Ví dụ tìm các giá trị lượng giác của góc 120°

Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat{xOM}\) = 120o. Gọi N, K tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

\(\text{Do } \widehat{xOM} = 120^\circ \text{ và } \widehat{xOK} = 90^\circ \text{ nên } \widehat{KOM} = 30^\circ \text{ và } \widehat{MON} = 60^\circ.\)

Từ bảng GTLG của một số góc đặc biệt:

Ta có: \(\cos 60^\circ = \frac{1}{2} \quad \text{và} \quad \cos 30^\circ = \frac{\sqrt{3}}{2}\)

Các tam giác MOK và MON là các tam giác vuông với cạnh huyền bằng 1

Suy ra ON = cos \(\widehat{MON} \cdot OM = \cos 60^\circ \cdot 1 = \frac{1}{2}\) và OK = cos \(\widehat{MOK} \cdot OM = \cos 30^\circ \cdot 1 = \frac{\sqrt{3}}{2}\)

Mặt khác, do điểm M nằm bên trái trục tung nên \(M \left( -\frac{1}{2}; \frac{\sqrt{3}}{2} \right)\)

Theo định nghĩa giá trị lượng giác ta có:

\(\sin 120^\circ = \frac{\sqrt{3}}{2}\)

\(\cos 120^\circ = -\frac{1}{2}\)

\(\tan 120^\circ = \frac{\sin 120^\circ}{\cos 120^\circ} = -\sqrt{3}\)

\(\cot 120^\circ = \frac{\cos 120^\circ}{\sin 120^\circ} = -\frac{1}{\sqrt{3}}\)

Vậy \(\sin 120^\circ = \frac{\sqrt{3}}{2}; \quad \cos 120^\circ = -\frac{1}{2}; \quad \tan 120^\circ = -\sqrt{3}; \quad \cot 120^\circ = -\frac{1}{\sqrt{3}}\).

– Ta có thể dùng máy tính bỏ túi để tính giá trị gần đúng của các giá trị lượng giác của một góc.

Cách dùng máy tính bỏ túi để tính giá trị gần đúng của các giá trị lượng giác

Ví dụ:

– Ta cũng có thể tìm được góc khi biết một giá trị lượng giác của góc đó.

Tìm góc khi biết một giá trị lượng giác bằng MTCT

Ví dụ:

Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Đối với hai góc bù nhau, α và \(180^\circ\) – α, ta có:

\(\sin (180^\circ – \alpha) = \sin \alpha\);

\(\cos (180^\circ – \alpha) = -\cos \alpha\);

\(\tan (180^\circ – \alpha) = -\tan \alpha \ (\alpha \neq 90^\circ)\);

\(\cot (180^\circ – \alpha) = -\cot \alpha \ (0^\circ < \alpha < 180^\circ)\).

Ví dụ:

Ta có \(30^\circ\) + \(60^\circ\) = \(90^\circ\) nên góc \(30^\circ\) và góc \(60^\circ\) là hai góc phụ nhau.

Khi đó:

\(\sin 30^\circ = \cos 60^\circ = \frac{1}{2}\)

\(\tan 30^\circ = \cot 60^\circ = \frac{\sqrt{3}}{3}\)

Các giá trị lượng giác của một góc là một phần quan trọng trong toán học mà bạn không thể bỏ qua. Hy vọng rằng những kiến thức và công thức các em đã học qua bài này sẽ giúp các em tự tin hơn khi giải các bài toán. Hãy tiếp tục khám phá thêm các bài học khác để mở rộng kiến thức của mình nhé.

<<Xem thêm>> Lý thuyết Toán 10 Bài 9: Tích của một vectơ với một số