Góc đối đỉnh là gì? Định nghĩa và tính chất bạn cần ghi nhớ

Trong chương trình Hình học lớp 7, khái niệm góc đối đỉnh là một trong những kiến thức nền tảng vô cùng quan trọng. Hiểu rõ góc đối đỉnh là gì, nắm vững định nghĩa và các tính chất liên quan không chỉ giúp học sinh giải quyết tốt các bài tập cơ bản mà còn tạo tiền đề vững chắc để tiếp thu những kiến thức hình học phức tạp hơn sau này.

Khái niệm Góc đối đỉnh là gì?

Để hiểu chính xác về , chúng ta cần bắt đầu từ định nghĩa cơ bản nhất của nó.

Góc đối đỉnh là gì?

Định nghĩa chính xác: Hai góc được gọi là đối đỉnh nếu mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Đây là mấu chốt quan trọng nhất để xác định hai góc có phải là đối đỉnh hay không.

Để hình dung rõ hơn, hãy xem xét một ví dụ đơn giản: Khi hai đường thẳng (ví dụ đường thẳng xx’ và yy’) cắt nhau tại một điểm (gọi là điểm O), chúng sẽ tạo thành bốn góc có chung đỉnh O (ví dụ: góc xOy, góc yOx’, góc x’Oy’, góc y’Ox). Trong trường hợp này:

• Cạnh Ox là tia đối của cạnh Ox’.
• Cạnh Oy là tia đối của cạnh Oy’.

Do đó, góc xOy và góc x’Oy’ là hai góc đối đỉnh. Tương tự, cạnh Ox là tia đối của Ox’, và cạnh Oy’ là tia đối của Oy, nên góc xOy’ và góc x’Oy cũng là một cặp góc đối đỉnh khác.

Điều kiện tiên quyết để hai góc là đối đỉnh chính là việc các cạnh tương ứng của chúng phải là các tia đối của nhau. Điều này có nghĩa là chúng phải cùng nằm trên một đường thẳng và có chung gốc O.

Tính chất quan trọng của góc đối đỉnh

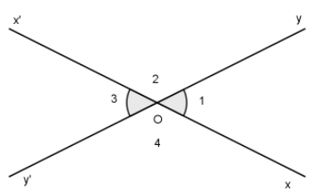
Tính chất của góc đối đỉnh

Nắm vững tính chất của góc đối đỉnh là chìa khóa để vận dụng hiệu quả khái niệm này vào giải toán. Tính chất quan trọng và được sử dụng nhiều nhất là:

Tính chất cơ bản nhất: Hai góc đối đỉnh thì bằng nhau.

Tại sao lại có tính chất này? Chúng ta có thể chứng minh một cách logic dựa vào kiến thức về góc kề bù (hai góc có chung một cạnh, hai cạnh còn lại là hai tia đối nhau và có tổng số đo bằng 180 độ).

Xét lại ví dụ hai đường thẳng xx’ và yy’ cắt nhau tại O:

1. Góc xOy và góc yOx’ là hai góc kề bù (vì Ox và Ox’ là hai tia đối, Oy là cạnh chung). Do đó: góc xOy + góc yOx’ = 180 độ.
2. Góc yOx’ và góc x’Oy’ cũng là hai góc kề bù (vì Oy và Oy’ là hai tia đối, Ox’ là cạnh chung). Do đó: góc yOx’ + góc x’Oy’ = 180 độ.
3. Từ (1) và (2), ta thấy: góc xOy + góc yOx’ = góc yOx’ + góc x’Oy’ (vì cùng bằng 180 độ).
4. Suy ra: góc xOy = góc x’Oy’.

Chứng minh tương tự, ta cũng có góc xOy’ = góc x’Oy. Đây là bằng chứng cho thấy tính chất “hai góc đối đỉnh thì bằng nhau” là hoàn toàn chính xác.

Ngoài ra, trong trường hợp đặc biệt khi hai đường thẳng cắt nhau và vuông góc với nhau, chúng sẽ tạo ra bốn góc vuông (90 độ). Khi đó, các cặp góc đối đỉnh đều là các góc vuông và đương nhiên chúng bằng nhau.

Việc ghi nhớ và vận dụng thành thạo tính chất này là cực kỳ quan trọng, giúp giải quyết nhanh chóng nhiều bài toán liên quan đến tính số đo góc hoặc chứng minh trong hình học.

Cách nhận biết hai góc đối đỉnh

Để xác định chính xác hai góc có phải là đối đỉnh hay không, học sinh cần dựa vào các dấu hiệu nhận biết sau đây, xuất phát trực tiếp từ định nghĩa:

• Dấu hiệu 1: Chung đỉnh. Hai góc phải có cùng một điểm đỉnh. Nếu hai góc có đỉnh khác nhau, chúng chắc chắn không phải là góc đối đỉnh.
• Dấu hiệu 2: Mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Đây là dấu hiệu cốt lõi và mang tính quyết định. Cần kiểm tra xem các tia tạo thành hai góc có phải là các cặp tia đối nhau qua đỉnh chung hay không. Ví dụ, nếu góc thứ nhất tạo bởi tia Oa và Ob, góc thứ hai tạo bởi tia Oc và Od, thì chúng đối đỉnh nếu Oa là tia đối của Oc (hoặc Od) và Ob là tia đối của Od (hoặc Oc), và chúng có chung đỉnh O.

Điều quan trọng là phải phân biệt rõ góc đối đỉnh với các loại góc khác có vẻ tương tự nhưng bản chất khác nhau:

• Góc kề bù: Chung đỉnh, có một cạnh chung, hai cạnh còn lại là hai tia đối nhau. Tổng số đo hai góc kề bù luôn bằng 180 độ. Hai góc đối đỉnh không phải là góc kề bù (trừ trường hợp đặc biệt các góc đều là 90 độ).
• Góc kề nhau: Chung đỉnh, có một cạnh chung, hai cạnh còn lại nằm về hai phía khác nhau của đường thẳng chứa cạnh chung. Góc kề nhau không nhất thiết phải có tổng bằng 180 độ và các cạnh không nhất thiết phải là tia đối.

Ví dụ kiểm tra nhanh: Trong hình vẽ có hai đường thẳng AB và CD cắt nhau tại M. Hãy xác định các cặp góc đối đỉnh. Trả lời: Dựa vào định nghĩa, ta có: – Góc AMC và góc BMD là đối đỉnh (cạnh MA là tia đối MB, MC là tia đối MD, chung đỉnh M). – Góc AMD và góc BMC là đối đỉnh (cạnh MA là tia đối MB, MD là tia đối MC, chung đỉnh M).

Các dạng bài tập thường gặp về góc đối đỉnh

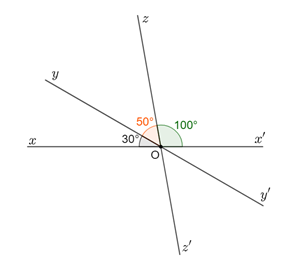
Các dạng bài tập thường gặp về góc đối đỉnh

Kiến thức về thường xuất hiện trong các dạng bài tập cơ bản sau:

• Dạng 1: Tính số đo góc. Đây là dạng bài tập phổ biến nhất. Đề bài thường cho biết số đo của một góc và yêu cầu tính số đo của góc đối đỉnh với nó hoặc các góc kề bù liên quan.Ví dụ: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Biết góc xOy = 60 độ. Tính số đo góc x’Oy’. Cách giải: Vì góc xOy và góc x’Oy’ là hai góc đối đỉnh nên theo tính chất, góc x’Oy’ = góc xOy = 60 độ.
• Dạng 2: Chứng minh hai góc bằng nhau. Trong các bài toán chứng minh hình học phức tạp hơn, việc nhận biết và sử dụng tính chất “hai góc đối đỉnh thì bằng nhau” thường là một bước quan trọng để đi đến kết luận cuối cùng. Nó cung cấp một luận cứ vững chắc để chứng minh sự bằng nhau của hai góc.
• Dạng 3: Nhận biết cặp góc đối đỉnh. Đề bài có thể cho một hình vẽ với nhiều đường thẳng cắt nhau, yêu cầu học sinh xác định đúng các cặp góc đối đỉnh. Kỹ năng cần thiết là quan sát cẩn thận, xác định các điểm giao và áp dụng đúng định nghĩa (tia đối, chung đỉnh).

Lưu ý khi giải bài tập về góc đối đỉnh:

• Đọc kỹ yêu cầu của đề bài.
• Nếu đề bài không cho hình vẽ sẵn, hãy vẽ hình một cách chính xác dựa trên mô tả. Việc vẽ hình đúng giúp trực quan hóa vấn đề và dễ dàng nhận biết các cặp góc hơn.
• Vận dụng chính xác định nghĩa và tính chất của góc đối đỉnh. Ghi rõ lý do (ví dụ: “Vì góc A và góc B là hai góc đối đỉnh nên góc A = góc B”).
• Phân biệt rõ ràng với góc kề bù, góc kề nhau để tránh nhầm lẫn.

XEM THÊM

• Góc Treitz là gì?
• Góc nhìn thứ nhất là gì?

Mở rộng và ứng dụng của góc đối đỉnh

Ứng dụng của góc đối đỉnh

Tuy là một khái niệm cơ bản, lại có vai trò quan trọng và ứng dụng rộng rãi trong hình học cũng như trong thực tế:

• Trong hình học phẳng: Kiến thức về góc đối đỉnh là nền tảng để xây dựng và chứng minh nhiều định lý, tính chất hình học phức tạp hơn. Ví dụ, nó được sử dụng khi chứng minh hai đường thẳng song song (thông qua góc so le trong, đồng vị mà một trong số đó đối đỉnh với góc đã biết), khi tính toán các góc trong các tứ giác đặc biệt như hình thang, hình bình hành, hình thoi…
• Trong thực tế: Hình ảnh của các cặp góc đối đỉnh xuất hiện khá nhiều xung quanh chúng ta. Bạn có thể thấy chúng ở:
  • Các giao lộ đường bộ, đường sắt nơi các con đường cắt nhau.
  • Các cấu trúc đan chéo như khung cửa sổ kiểu mắt cáo, hàng rào lưới B40.
  • Nan hoa của bánh xe đạp giao nhau tại trục.
  • Trong một số hiện tượng quang học, dù không hoàn toàn chính xác là góc đối đỉnh theo định nghĩa toán học, sự bằng nhau của góc tới và góc phản xạ trên gương phẳng có nét tương đồng về mặt hình ảnh khi vẽ tia sáng.
• Liên kết với các khái niệm khác: Hiểu về góc đối đỉnh giúp củng cố và liên kết với các kiến thức quan trọng khác như: Hai đường thẳng song song, Góc so le trong, Góc đồng vị. Mối quan hệ giữa các loại góc này thường được khai thác trong các bài toán tổng hợp.

Câu hỏi thường gặp về góc đối đỉnh (FAQ)

Dưới đây là một số câu hỏi thường gặp giúp bạn hiểu rõ hơn về :

Q1: Hai góc bằng nhau có phải luôn là góc đối đỉnh không?

A: Không. Hai góc bằng nhau chưa chắc đã là hai góc đối đỉnh. Ví dụ, hai góc cùng bằng 30 độ nhưng nằm ở hai vị trí hoàn toàn khác nhau, không có đỉnh chung hoặc không thỏa mãn điều kiện cạnh là tia đối của nhau thì không phải là góc đối đỉnh. Tính chất chỉ phát biểu theo một chiều: “Nếu hai góc là đối đỉnh THÌ chúng bằng nhau”, chứ không phải ngược lại.

Q2: Góc đối đỉnh có phải luôn nhỏ hơn 180 độ không?

A: Có. Góc đối đỉnh được tạo bởi hai đường thẳng cắt nhau. Mỗi góc trong bốn góc được tạo thành đều nhỏ hơn góc bẹt (180 độ). Góc bẹt được tạo bởi hai tia đối nhau, không phải là kết quả trực tiếp của hai đường thẳng *cắt* nhau theo cách tạo ra góc đối đỉnh thông thường.

Q3: Làm sao để vẽ hai góc đối đỉnh chính xác?

A: Cách đơn giản và chính xác nhất là vẽ hai đường thẳng bất kỳ cắt nhau tại một điểm. Giao điểm đó chính là đỉnh chung của các cặp góc đối đỉnh được tạo thành. Bạn chỉ cần vẽ một đường thẳng, sau đó vẽ một đường thẳng khác cắt đường thẳng đầu tiên là sẽ có ngay các cặp góc đối đỉnh.

Q4: Góc kề bù với một trong hai góc đối đỉnh có bằng góc kề bù với góc đối đỉnh còn lại không?

A: Có. Giả sử góc O1 và O3 là đối đỉnh (O1 = O3), góc O2 kề bù với O1 (O1 + O2 = 180 độ), góc O4 kề bù với O3 (O3 + O4 = 180 độ). Vì O1 = O3 nên suy ra O2 = O4. Điều này hoàn toàn hợp lý vì O2 và O4 cũng chính là một cặp góc đối đỉnh khác được tạo thành.

Kết luận

Qua bài viết này, hy vọng các bạn học sinh đã có cái nhìn đầy đủ và rõ ràng về góc đối đỉnh là gì, bao gồm định nghĩa chính xác, tính chất quan trọng nhất (hai góc đối đỉnh thì bằng nhau), cách nhận biết và các dạng bài tập liên quan. Việc nắm vững khái niệm tưởng chừng đơn giản này là vô cùng cần thiết.