Góc vuông là gì? Định nghĩa, ký hiệu và ví dụ minh họa

Góc vuông là một khái niệm cơ bản trong hình học, đóng vai trò quan trọng trong nhiều lĩnh vực toán học và ứng dụng thực tiễn. Bài viết này sẽ giúp bạn hiểu rõ về định nghĩa, ký hiệu và các ví dụ minh họa về góc vuông, từ đó nắm vững kiến thức nền tảng này trong hình học.

Định nghĩa góc vuông trong hình học

Trong hình học, góc vuông là góc có số đo chính xác bằng 90 độ (hoặc π/2 radian). Đây là một trong những loại góc cơ bản và quan trọng nhất trong toán học, đặc biệt là trong hình học phẳng và không gian.

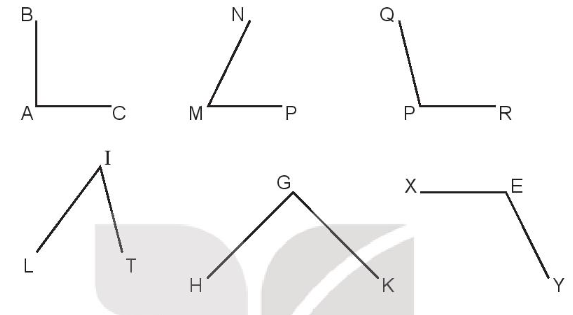
Định nghĩa góc vuông trong hình học

Khi hai đường thẳng cắt nhau tạo thành góc vuông, chúng được gọi là vuông góc với nhau. Hai đường thẳng vuông góc với nhau tạo ra bốn góc bằng nhau, mỗi góc đều là góc vuông.

Đặc điểm của góc vuông

• Số đo chuẩn: Góc vuông luôn có số đo chính xác 90 độ hay π/2 radian
• Tính đối xứng: Khi hai đường thẳng tạo thành góc vuông, chúng chia mặt phẳng thành bốn phần bằng nhau
• Tổng với góc vuông khác: Hai góc vuông cộng lại tạo thành góc bằng (180 độ)
• Quan hệ với góc khác: Góc vuông lớn hơn góc nhọn (nhỏ hơn 90 độ) và nhỏ hơn góc tù (lớn hơn 90 độ)

Ký hiệu của góc vuông trong toán học

Trong các bài toán và hình vẽ hình học, góc vuông thường được biểu thị bằng các ký hiệu đặc trưng để dễ dàng nhận biết và phân biệt với các loại góc khác.

Các cách ký hiệu góc vuông phổ biến

• Ký hiệu vuông nhỏ (⊾): Đây là ký hiệu phổ biến nhất, thường được vẽ tại đỉnh của góc vuông
• Ký hiệu 90°: Ghi trực tiếp số đo 90° vào góc để chỉ rõ đó là góc vuông
• Ký hiệu π/2: Trong hệ đo radian, góc vuông được ký hiệu là π/2
• Ký hiệu ⊥: Dùng để biểu thị hai đường thẳng vuông góc với nhau

Sự khác biệt giữa ký hiệu góc vuông và các loại góc khác

Ký hiệu góc vuông có những đặc điểm riêng giúp phân biệt với các loại góc khác:

• Góc nhọn (< 90°): Thường không có ký hiệu đặc biệt, chỉ ghi số đo
• Góc tù (> 90°): Không có ký hiệu vuông, đôi khi được biểu thị bằng cung tròn lớn hơn
• Góc bằng (180°): Thường được biểu thị bằng đường thẳng
• Góc vuông (90°): Luôn có ký hiệu vuông nhỏ (⊾) tại đỉnh góc

Ví dụ về góc vuông trong hình học phẳng

Góc vuông xuất hiện trong nhiều hình dạng và cấu trúc hình học phẳng. Dưới đây là một số ví dụ tiêu biểu về sự hiện diện của góc vuông trong hình học phẳng.

Góc vuông trong hình chữ nhật và hình vuông

Hình chữ nhật và hình vuông là những ví dụ điển hình và quen thuộc nhất về hình có góc vuông:

• Hình chữ nhật: Có 4 góc vuông, các cạnh kề tạo thành góc 90 độ với nhau
• Hình vuông: Là trường hợp đặc biệt của hình chữ nhật với 4 cạnh bằng nhau và 4 góc đều là góc vuông
• Hình thoi có góc vuông: Khi hình thoi có một góc vuông, thì góc đối diện cũng là góc vuông, và hình thoi đó chính là hình vuông

Góc vuông trong tam giác vuông

Góc vuông trong tam giác vuông

Tam giác vuông là một trong những hình học cơ bản và quan trọng nhất có chứa góc vuông:

• Định nghĩa: Tam giác vuông là tam giác có một góc vuông (90°)
• Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
• Tam giác vuông cân: Là tam giác vừa vuông vừa cân, có hai cạnh góc vuông bằng nhau và hai góc nhọn bằng 45°
• Tam giác vuông đặc biệt: Các tam giác vuông với tỷ lệ cạnh đặc biệt như 3:4:5, 5:12:13, 8:15:17

Góc vuông trong không gian ba chiều

Khái niệm góc vuông không chỉ giới hạn trong hình học phẳng mà còn mở rộng ra không gian ba chiều, nơi nó đóng vai trò quan trọng trong việc xác định các mối quan hệ hình học trong không gian.

Đường thẳng và mặt phẳng vuông góc

Trong không gian ba chiều, góc vuông xuất hiện trong các mối quan hệ giữa đường thẳng và mặt phẳng:

• Đường thẳng vuông góc với mặt phẳng: Khi đường thẳng tạo góc 90° với mọi đường thẳng nằm trên mặt phẳng và đi qua điểm giao của đường thẳng với mặt phẳng
• Hai mặt phẳng vuông góc: Khi góc giữa hai mặt phẳng (đo bởi góc giữa hai đường thẳng vuông góc với đường giao của hai mặt phẳng) bằng 90°
• Góc nhị diện vuông: Góc giữa hai nửa mặt phẳng có chung đường biên khi góc đó bằng 90°

Góc vuông trong các khối đa diện

Góc vuông xuất hiện trong nhiều khối đa diện thường gặp:

• Hình hộp chữ nhật: Có 12 cạnh, 8 đỉnh và tất cả các góc đều là góc vuông
• Hình lập phương: Là trường hợp đặc biệt của hình hộp chữ nhật với tất cả các cạnh bằng nhau
• Hình chóp đều có đáy là hình vuông: Có 4 góc vuông ở đáy
• Hình trụ và hình nón có trục vuông góc với đáy: Trục của hình tạo góc vuông với mặt phẳng đáy

XEM THÊM

• Góc Treitz là gì?
• Góc nhìn thứ nhất là gì?

Ứng dụng của góc vuông trong thực tế

Góc vuông không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và trong các lĩnh vực chuyên môn.

Ứng dụng của góc vuông

Góc vuông trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc và xây dựng, góc vuông đóng vai trò thiết yếu:

• Kết cấu xây dựng: Tường, sàn, trần nhà thường được thiết kế vuông góc với nhau để tạo độ ổn định và thẩm mỹ
• Công cụ đo góc vuông: Thước ê-ke, thước thợ, máy đo laser được sử dụng để đảm bảo các kết cấu vuông góc
• Nguyên lý cân bằng: Các cột trụ thường được xây dựng vuông góc với mặt đất để đảm bảo khả năng chịu lực tối ưu
• Thiết kế nội thất: Tủ, bàn, ghế và các vật dụng thường được thiết kế với các góc vuông để tạo sự ổn định và phù hợp với không gian

Góc vuông trong đời sống hàng ngày

Trong cuộc sống hàng ngày, chúng ta thường xuyên tiếp xúc với góc vuông:

• Đồ dùng gia đình: Tủ lạnh, tivi, máy tính, sách vở thường có hình dạng chữ nhật với các góc vuông
• Thiết kế đường phố: Nhiều thành phố được quy hoạch với các đường phố cắt nhau tạo thành góc vuông
• Thiết bị điện tử: Bo mạch, chip máy tính thường được thiết kế với các góc vuông để tối ưu không gian
• Thể thao: Sân bóng đá, sân tennis, bàn bóng bàn đều có hình chữ nhật với các góc vuông

Cách xác định và vẽ góc vuông chính xác

Việc xác định và vẽ góc vuông chính xác là kỹ năng quan trọng trong học tập và các ứng dụng thực tế. Dưới đây là một số phương pháp để xác định và vẽ góc vuông một cách chính xác.

Các công cụ đo góc vuông

Có nhiều công cụ được thiết kế đặc biệt để đo và vẽ góc vuông:

• Thước ê-ke: Công cụ hình tam giác có một góc 90° dùng để vẽ các đường vuông góc
• Compa: Kết hợp với thước thẳng để vẽ đường vuông góc từ một điểm đến một đường thẳng
• Thước đo góc (thước protractor): Dùng để đo chính xác góc 90°
• Thước thợ (square): Công cụ hình chữ L dùng trong xây dựng để đảm bảo các góc vuông
• Máy đo laser: Công nghệ hiện đại giúp xác định đường thẳng và góc vuông chính xác

Phương pháp vẽ góc vuông không cần dụng cụ đặc biệt

Khi không có sẵn dụng cụ chuyên dụng, bạn vẫn có thể vẽ góc vuông bằng các phương pháp sau:

• Phương pháp gấp giấy: Gấp một tờ giấy đôi rồi gấp lại một lần nữa, khi mở ra bạn sẽ có các nếp gấp tạo thành góc vuông
• Phương pháp tam giác 3-4-5: Dựa trên định lý Pythagoras, tạo tam giác với các cạnh có tỷ lệ 3:4:5 sẽ cho một góc vuông
• Phương pháp đường tròn: Vẽ đường tròn, nối tâm với một điểm trên đường tròn, sau đó vẽ tiếp tuyến tại điểm đó sẽ được góc vuông
• Phương pháp đường chéo: Vẽ hình vuông hoặc hình chữ nhật, các đường chéo cắt nhau tạo bốn góc bằng nhau, mỗi góc là 90°

Câu hỏi thường gặp về góc vuông

Góc vuông có những đặc điểm gì khác biệt so với các loại góc khác?

Góc vuông có số đo chính xác 90 độ hoặc π/2 radian, là ranh giới giữa góc nhọn và góc tù. Đây là góc cơ bản trong hình học, tạo nên tính vuông góc giữa hai đường thẳng. Khi hai đường thẳng tạo thành góc vuông, chúng chia mặt phẳng thành bốn phần bằng nhau, mỗi phần có góc 90°. Góc vuông là nền tảng cho nhiều định lý quan trọng như định lý Pythagoras và là cơ sở cho các phép đo, xây dựng trong thực tế.

Làm thế nào để chứng minh hai đường thẳng vuông góc với nhau?

Có nhiều phương pháp để chứng minh hai đường thẳng vuông góc với nhau:

• Sử dụng đo góc trực tiếp: Nếu góc giữa hai đường thẳng đo được chính xác 90°
• Sử dụng hệ số góc: Hai đường thẳng có hệ số góc m₁ và m₂ vuông góc với nhau nếu m₁ × m₂ = -1
• Sử dụng tọa độ: Hai vector vuông góc nếu tích vô hướng của chúng bằng 0
• Sử dụng định lý Pythagoras: Trong tam giác, nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại, thì góc đối diện với cạnh đó là góc vuông
• Sử dụng tính chất đường tròn: Góc nội tiếp trong nửa đường tròn luôn là góc vuông

Tại sao góc vuông lại quan trọng trong toán học và ứng dụng thực tế?

Góc vuông đóng vai trò quan trọng vì nhiều lý do:

• Nền tảng hình học: Là cơ sở cho nhiều định lý và tính chất hình học
• Đơn giản hóa tính toán: Trong hệ tọa độ vuông góc, các phép tính trở nên đơn giản hơn
• Ổn định kết cấu: Trong xây dựng, góc vuông tạo độ ổn định tối ưu cho các công trình
• Tối ưu không gian: Thiết kế với góc vuông giúp tận dụng không gian hiệu quả
• Chuẩn mực thẩm mỹ: Trong nghệ thuật và thiết kế, góc vuông tạo cảm giác cân đối, hài hòa
• Ứng dụng rộng rãi: Xuất hiện trong gần như mọi lĩnh vực từ khoa học, kỹ thuật đến đời sống hàng ngày

Kết luận

Việc hiểu rõ về góc vuông, cách xác định và vẽ góc vuông chính xác không chỉ giúp học sinh nắm vững kiến thức hình học cơ bản mà còn phát triển tư duy không gian và kỹ năng ứng dụng toán học vào thực tế. Đây chính là lý do vì sao góc vuông luôn là một chủ đề quan trọng trong chương trình giáo dục toán học từ cấp tiểu học đến các bậc học cao hơn.