Với tóm tắt lý thuyết Toán 11 Bài 11: Hai đường thẳng song song sách Kết nối tri thức chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.
Lý thuyết Hai đường thẳng song song Lớp 11
Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng a và b trong không gian.
– Nếu a và b nằm trong cùng một mặt phẳng, ta gọi chúng là đồng phẳng. Trong trường hợp này, a và b có thể cắt nhau, song song hoặc trùng nhau.
– Nếu a và b không thuộc cùng một mặt phẳng, ta nói chúng chéo nhau. Khi đó, ta cũng có thể nói a chéo với b hoặc b chéo với a.
Trường hợp 1: a và b nằm trong cùng một mặt phẳng.
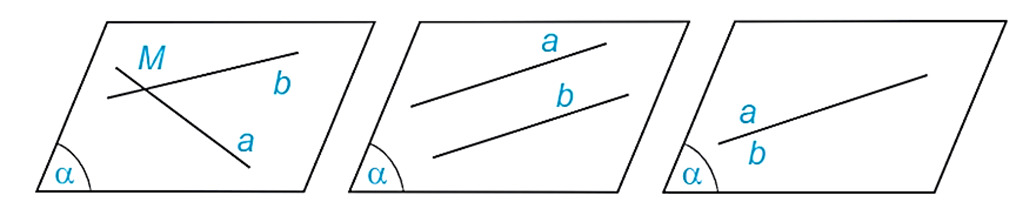
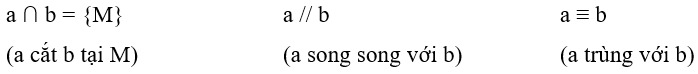
Trường hợp 2: a và b không nằm trong bất kỳ mặt phẳng nào.
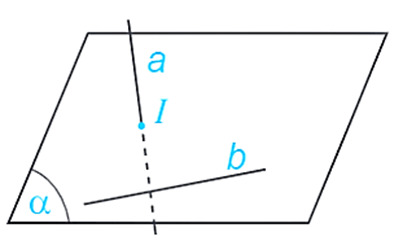
Nhận xét:
– Hai đường thẳng song song là hai đường nằm trong cùng một mặt phẳng nhưng không giao nhau tại bất kỳ điểm nào.
– Có duy nhất một mặt phẳng chứa hai đường thẳng song song.
Lưu ý: Hai đường thẳng không giao nhau có thể là song song hoặc chéo nhau.
Ví dụ: Cho hình tứ diện SABC. Chỉ ra các cặp đường thẳng chéo nhau có trong hình tứ diện này?
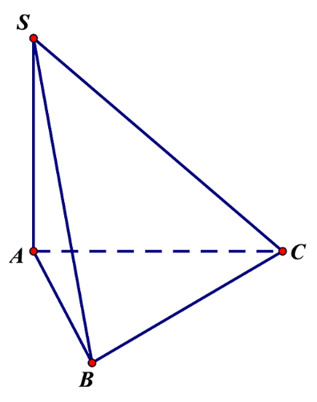
Hướng dẫn giải:
Nếu hai đường thẳng SA và BC không chéo nhau, thì chúng phải nằm trong cùng một mặt phẳng, dẫn đến việc bốn điểm S, A, B, C đồng phẳng, điều này mâu thuẫn với giả thiết rằng SABC là một tứ diện.
Vì vậy, hai đường thẳng SA và BC phải chéo nhau.
Lập luận tương tự, ta có thể kết luận rằng các cặp đường thẳng chéo nhau khác là SB và AC, SC và AB.
Tính chất của hai đường thẳng song song
Tính chất 1: Trong không gian, qua một điểm không thuộc đường thẳng cho trước, chỉ có duy nhất một đường thẳng song song với đường thẳng đó.
Tính chất 2: Trong không gian, nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng cũng song song với nhau.
Tính chất 3: Khi ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt, thì ba giao tuyến này hoặc đồng quy tại một điểm, hoặc đôi một song song.
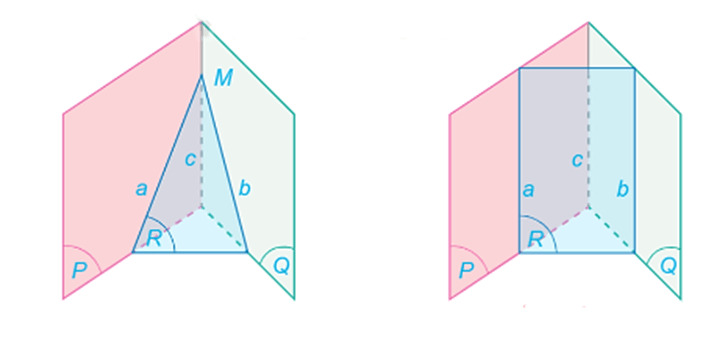
Lưu ý: Nếu hai mặt phẳng chứa hai đường thẳng song song, thì giao tuyến của chúng (nếu có) sẽ song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng.
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Xác định giao tuyến:
a) (SAC) và (SBD).
b) (SAB) và (SCD).
Hướng dẫn giải
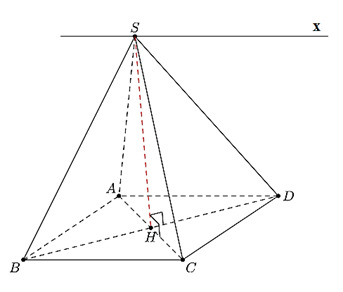
Gọi H là điểm giao của AC và BD.
a) Cả hai mặt phẳng (SAC) và (SBD) đều đi qua đỉnh S.
Đồng thời, H là giao điểm của AC và BD, tức là H = AC ∩ BD, nên H cũng là điểm chung của hai mặt phẳng này H = (SAC) ∩ (SBD).
Vì vậy: SH = (SAC) ∩ (SBD).
⇒ Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng SH.
b) Hai mặt phẳng (SAB) và (SCD) có điểm chung là S và cùng chứa hai đường thẳng song song AB và CD.
Do đó, giao tuyến của hai mặt phẳng này là đường thẳng Sx, đi qua điểm S và song song với AB và CD.
Có thể bạn quan tâm:
Sơ đồ tư duy tóm tắt lý thuyết về hai đường thẳng song song
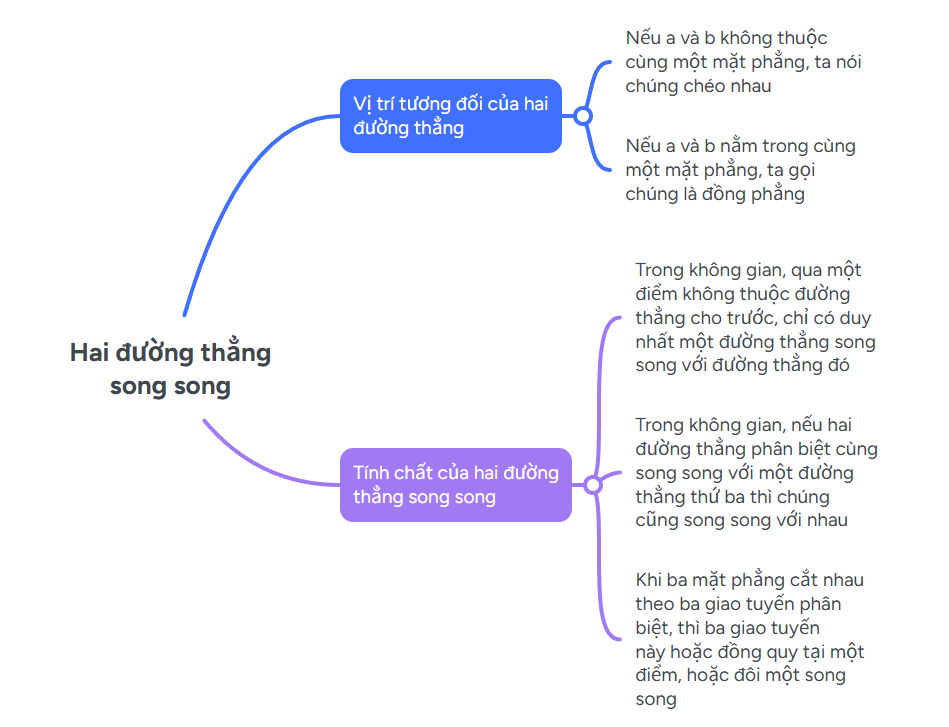










 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa