Hai lực đồng quy là gì? Công thức xác định lực đồng quy

Trong chương trình Vật lý phổ thông, khái niệm về lực và các loại lực là nền tảng cơ bản giúp học sinh hiểu rõ hơn về thế giới cơ học xung quanh. Một trong những khái niệm quan trọng đó là hai lực đồng quy. Vậy hai lực đồng quy là gì? Làm thế nào để xác định hợp lực của chúng? Bài viết này sẽ cung cấp kiến thức chi tiết, dễ hiểu và công thức cần thiết để bạn nắm vững chủ đề này.

Khái niệm hai lực đồng quy là gì?

Hai lực đồng quy là hai lực có đường tác dụng (hay còn gọi là giá của lực) cùng đi qua một điểm. Nói cách khác, nếu ta kéo dài đường thẳng chứa vector của hai lực đó, chúng sẽ cắt nhau tại một điểm duy nhất. Điểm cắt nhau này chính là điểm đồng quy của hai lực.

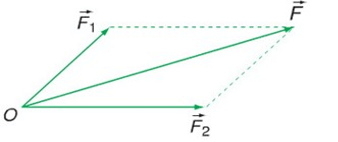
Hai lực đồng quy là gì?

Cần lưu ý rằng, điểm đồng quy không nhất thiết phải là điểm đặt của cả hai lực lên vật. Các lực có thể có điểm đặt khác nhau trên vật, nhưng miễn là đường tác dụng của chúng giao nhau tại một điểm thì chúng vẫn được coi là đồng quy. Ví dụ, khi hai người cùng kéo một chiếc thuyền bằng hai sợi dây buộc vào hai điểm khác nhau trên mũi thuyền, nếu hướng kéo của họ làm cho đường kéo dài của hai sợi dây cắt nhau tại một điểm phía trước thuyền, thì hai lực kéo đó là đồng quy tại điểm giao nhau đó.

Khái niệm hai lực đồng quy là cực kỳ quan trọng trong việc phân tích và tổng hợp lực tác dụng lên vật rắn. Nó là cơ sở để áp dụng các quy tắc tìm hợp lực, giúp đơn giản hóa việc nghiên cứu trạng thái cân bằng hoặc chuyển động của vật dưới tác dụng của nhiều lực.

Việc hiểu rõ hai lực đồng quy là gì giúp phân biệt chúng với các trường hợp khác như lực song song (có đường tác dụng song song) hay các lực không đồng quy (đường tác dụng không cắt nhau tại cùng một điểm), vốn đòi hỏi các phương pháp phân tích khác.

Đặc điểm của hai lực đồng quy

Hai lực đồng quy có những đặc điểm cơ bản và quan trọng giúp chúng ta nhận biết và phân tích tác dụng của chúng lên vật. Các đặc điểm chính bao gồm:

• Điểm đồng quy chung: Đây là đặc điểm cốt lõi. Đường tác dụng của hai lực F&x20D7;₁ và F&x20D7;₂ phải cắt nhau tại một điểm O. Điểm O này được gọi là điểm đồng quy. Điều này ngụ ý rằng tác dụng của hai lực này có thể được xem xét tập trung tại điểm đó khi phân tích chuyển động tịnh tiến hoặc điều kiện cân bằng của vật.
• Tác dụng đồng thời: Hai lực này cùng tác động lên vật tại cùng một thời điểm. Hiệu quả tác dụng của chúng không phải là sự cộng dồn tuần tự mà là sự kết hợp tức thời.
• Gây ra hiệu ứng tổng hợp (Hợp lực): Khi tác dụng lên một vật, hai lực đồng quy sẽ gây ra một hiệu ứng tương đương với hiệu ứng của một lực duy nhất gọi là hợp lực (F&x20D7;). Hợp lực này được xác định bằng cách tổng hợp vector của hai lực thành phần theo các quy tắc nhất định (chủ yếu là quy tắc hình bình hành).

Việc xác định chính xác hợp lực này là chìa khóa để áp dụng Định luật II Newton, dự đoán gia tốc hoặc xác định điều kiện cân bằng của vật.

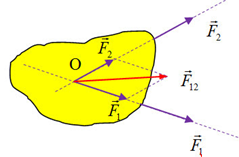
Đặc điểm của hai lực đồng quy

Công thức xác định hợp lực của hai lực đồng quy

Để xác định tác dụng tổng hợp của hai lực đồng quy F&x20D7;₁ và F&x20D7;₂ lên một vật, ta cần tìm hợp lực F&x20D7; của chúng. Hợp lực là một vector lực duy nhất có tác dụng hoàn toàn giống như tác dụng của cả hai lực thành phần đó. Phương pháp phổ biến và trực quan nhất để tìm hợp lực của hai lực đồng quy là sử dụng Quy tắc hình bình hành.

Quy tắc hình bình hành

Quy tắc hình bình hành phát biểu rằng: Nếu hai lực đồng quy F&x20D7;₁ và F&x20D7;₂ được biểu diễn bằng hai vector có chung điểm gốc (tại điểm đồng quy O), thì vector hợp lực F&x20D7; của chúng được biểu diễn bằng vector đường chéo của hình bình hành mà hai cạnh kề là hai vector F&x20D7;₁ và F&x20D7;₂, và đường chéo này cũng xuất phát từ điểm gốc O.

Các bước thực hiện:

1. Từ điểm đồng quy O, vẽ hai vector F&x20D7;₁ và F&x20D7;₂ biểu diễn hai lực đồng quy về phương, chiều và độ lớn (theo một tỉ lệ xích nhất định).
2. Từ ngọn của vector F&x20D7;₁, vẽ một đường thẳng song song với giá của vector F&x20D7;₂. Từ ngọn của vector F&x20D7;₂, vẽ một đường thẳng song song với giá của vector F&x20D7;₁. Hai đường thẳng này cắt nhau tại một điểm, tạo thành một hình bình hành.
3. Vẽ vector đường chéo F&x20D7; của hình bình hành, có gốc tại O và ngọn tại điểm cắt nhau nói trên. Vector F&x20D7; chính là vector hợp lực cần tìm: F&x20D7; = F&x20D7;₁ + F&x20D7;₂.

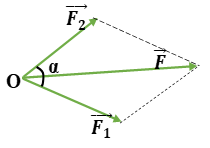
Quy tắc hình bình hành

Công thức tính độ lớn hợp lực

Từ quy tắc hình bình hành và sử dụng định lý hàm số cosin trong tam giác tạo bởi F&x20D7;₁, F&x20D7;₂ và F&x20D7;, ta có thể xác định được độ lớn của hợp lực F. Công thức tổng quát như sau:

F2 = F12 + F22 + 2 * F1 * F2 * cos(α)

Trong đó:

• F là độ lớn của hợp lực.
• F₁ và F₂ lần lượt là độ lớn của hai lực thành phần.
• α là góc tạo bởi hai vector lực F&x20D7;₁ và F&x20D7;₂ (0° ≤ α ≤ 180°).

Công thức này cho phép tính toán chính xác độ lớn của hợp lực khi biết độ lớn của hai lực thành phần và góc giữa chúng. Phương và chiều của hợp lực được xác định qua hình vẽ theo quy tắc hình bình hành hoặc tính toán dựa trên các hệ thức lượng trong tam giác.

Các trường hợp đặc biệt

Công thức tổng quát trên có thể được đơn giản hóa trong một số trường hợp đặc biệt của góc α:

• Khi hai lực cùng phương, cùng chiều (α = 0°): Lúc này cos(0°) = 1. Công thức trở thành F² = F₁² + F₂² + 2*F₁*F₂ = (F₁ + F₂)². Do đó, F = F1 + F2. Hợp lực có độ lớn bằng tổng độ lớn hai lực thành phần và cùng phương, cùng chiều với chúng.
• Khi hai lực cùng phương, ngược chiều (α = 180°): Lúc này cos(180°) = -1. Công thức trở thành F² = F₁² + F₂² – 2*F₁*F₂ = (F₁ – F₂)². Do đó, F = |F1 - F2|. Hợp lực có độ lớn bằng hiệu độ lớn hai lực thành phần, cùng phương và cùng chiều với lực có độ lớn lớn hơn.
• Khi hai lực vuông góc (α = 90°): Lúc này cos(90°) = 0. Công thức trở thành F² = F₁² + F₂². Do đó, F = √(F12 + F22) (Định lý Pytago). Hợp lực là đường chéo của hình chữ nhật tạo bởi hai lực thành phần.
• Khi hai lực có độ lớn bằng nhau (F₁ = F₂): Công thức trở thành F² = 2*F₁² + 2*F₁²*cos(α) = 2*F₁²*(1 + cos(α)). Sử dụng công thức hạ bậc cos(α) = 2*cos²(α/2) – 1, ta có F² = 2*F₁² * (2*cos²(α/2)) = 4*F₁²*cos²(α/2). Do đó, F = 2 * F1 * |cos(α/2)|. Vì 0° ≤ α ≤ 180° nên 0° ≤ α/2 ≤ 90°, suy ra cos(α/2) ≥ 0. Vậy F = 2 * F1 * cos(α/2). Trong trường hợp này, hợp lực nằm trên đường phân giác của góc α.

Việc nắm vững các trường hợp đặc biệt này giúp giải nhanh nhiều bài toán vật lý liên quan đến hai lực đồng quy.

Ví dụ thực tế về hai lực đồng quy

Khái niệm hai lực đồng quy không chỉ tồn tại trong sách giáo khoa mà còn xuất hiện rất nhiều trong đời sống hàng ngày và các ứng dụng kỹ thuật. Dưới đây là một số ví dụ điển hình:

• Trò chơi kéo co: Lực kéo của hai đội tác dụng lên sợi dây có thể xem là hai lực đồng quy tại một điểm (thường là điểm giữa của sợi dây hoặc vị trí đánh dấu). Hợp lực của hai lực này sẽ quyết định đội nào chiến thắng.
• Vật được treo bởi hai sợi dây: Một bức tranh, một chiếc đèn chùm hay bất kỳ vật nào được treo bằng hai sợi dây không song song. Trọng lực P&x20D7; của vật hướng xuống dưới, và hai lực căng T&x20D7;₁, T&x20D7;₂ của hai sợi dây hướng lên trên dọc theo dây. Ba lực này (trọng lực và hai lực căng) thường đồng quy tại điểm treo vật. Để vật cân bằng, hợp lực của hai lực căng phải cân bằng với trọng lực.
• Đẩy một chiếc tủ trên sàn: Khi bạn đẩy tủ, lực đẩy của bạn và lực ma sát của sàn nhà tác dụng lên tủ. Nếu xem tủ là một chất điểm, hai lực này thường được coi là đồng quy tại trọng tâm của mặt đáy tủ.
• Cây cầu dây văng: Lực căng từ các dây văng tác dụng lên đỉnh cột tháp cầu. Các lực căng này cùng với lực nén từ mặt cầu truyền xuống đều đồng quy tại các điểm nút trên cột tháp, đòi hỏi tính toán cẩn thận để đảm bảo sự ổn định.
• Lái thuyền buồm: Lực đẩy của gió tác dụng lên cánh buồm và lực cản của nước tác dụng lên thân thuyền là các yếu tố quyết định hướng di chuyển. Trong phân tích đơn giản, các lực này có thể được xem xét như các lực đồng quy để xác định hướng và tốc độ của thuyền.

Hiểu và áp dụng quy tắc tổng hợp hai lực đồng quy giúp chúng ta phân tích chính xác các tình huống này, từ việc xác định độ lớn lực căng dây cần thiết, tính toán sự ổn định của kết cấu, đến việc dự đoán chuyển động của vật.

XEM THÊM

• H2s là chất gì?
• Gốc tọa độ là gì?

Phân biệt hai lực đồng quy và các trường hợp khác

Để tránh nhầm lẫn và áp dụng đúng các nguyên tắc vật lý, điều quan trọng là phải phân biệt rõ ràng giữa hai lực đồng quy với các cặp lực khác thường gặp:

Hai lực đồng quy vs. Hai lực cân bằng

• Điểm chung: Hai lực cân bằng là một trường hợp đặc biệt của hai lực đồng quy.
• Điểm khác biệt cốt lõi:
  • Hai lực đồng quy: Chỉ cần có đường tác dụng cắt nhau tại một điểm. Hợp lực của chúng có thể khác không (gây ra gia tốc) hoặc bằng không.
  • Hai lực cân bằng: Bắt buộc phải là hai lực đồng quy, cùng tác dụng vào một vật, có cùng độ lớn, cùng phương, nhưng ngược chiều. Hợp lực của hai lực cân bằng luôn luôn bằng không (F = |F₁ – F₂| = 0 vì F₁ = F₂ và α = 180°). Chúng làm cho vật đứng yên hoặc chuyển động thẳng đều.
• Ví dụ: Khi bạn đứng yên trên mặt đất, trọng lực P&x20D7; (Trái Đất hút bạn) và phản lực N&x20D7; (mặt đất đẩy bạn lên) là hai lực cân bằng. Chúng đồng quy (tại trọng tâm của bạn), cùng phương, ngược chiều, cùng độ lớn.

Hai lực đồng quy vs. Hai lực song song

• Điểm khác biệt cơ bản:
  • Hai lực đồng quy: Đường tác dụng (giá) cắt nhau tại một điểm.
  • Hai lực song song: Đường tác dụng (giá) song song với nhau, không bao giờ cắt nhau.
• Phương pháp tổng hợp: Quy tắc tổng hợp hợp lực cho hai lực song song (cùng chiều hoặc ngược chiều) khác hoàn toàn với quy tắc hình bình hành dùng cho hai lực đồng quy. Quy tắc tổng hợp lực song song liên quan đến việc tìm điểm đặt của hợp lực trên đường thẳng nối hai điểm đặt của lực thành phần và độ lớn hợp lực tính toán khác.
• Ví dụ: Lực mà hai tay người gánh hàng tác dụng lên đòn gánh là hai lực song song cùng chiều.

Hai lực đồng quy vs. Lực và phản lực (Định luật III Newton)

• Điểm khác biệt cơ bản:
  • Hai lực đồng quy: Cùng tác dụng lên một vật.
  • Lực và phản lực: Luôn xuất hiện thành cặp, tác dụng lên hai vật tương tác khác nhau. Chúng có cùng độ lớn, cùng phương, ngược chiều nhưng không bao giờ tác dụng lên cùng một vật.
• Hậu quả: Vì tác dụng lên hai vật khác nhau, lực và phản lực không bao giờ cân bằng nhau (không triệt tiêu lẫn nhau khi xét chuyển động của từng vật) và chúng không phải là lực đồng quy theo định nghĩa (vì không cùng tác dụng lên một vật).
• Ví dụ: Khi bạn dùng tay đẩy vào tường (lực F&x20D7;), tường cũng đẩy lại tay bạn một lực (F&x20D7;’). F&x20D7; tác dụng lên tường, F&x20D7;’ tác dụng lên tay bạn. Đây là cặp lực – phản lực, không phải hai lực đồng quy tác dụng lên tường hay lên tay bạn.

Ứng dụng của việc xác định hợp lực hai lực đồng quy

Việc xác định hợp lực của hai lực đồng quy không chỉ là một bài toán lý thuyết trong Vật lý mà còn có vô số ứng dụng thực tiễn quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật:

• Kỹ thuật xây dựng và kiến trúc: Đây là lĩnh vực ứng dụng rõ rệt nhất. Các kỹ sư sử dụng nguyên tắc tổng hợp lực đồng quy để:
  • Tính toán lực tác dụng lên các nút (khớp nối) của các giàn thép, mái vòm, khung nhà.
  • Phân tích lực căng trong các dây cáp của cầu treo, cầu dây văng.
  • Đảm bảo sự ổn định và khả năng chịu lực của các kết cấu dưới tác động của trọng lực, tải trọng, gió bão…
• Thiết kế cơ khí:
  • Phân tích lực tại các khớp nối, ổ trục, bản lề trong máy móc, robot.
  • Tính toán lực cần thiết để giữ cân bằng hoặc di chuyển các bộ phận cơ khí.
  • Thiết kế các giá đỡ, khung chịu lực cho thiết bị.
• Phân tích chuyển động (Động lực học):
  • Áp dụng Định luật II Newton (F&x20D7;_{hợp lực} = ma&x20D7;): Bằng cách tìm hợp lực của tất cả các lực đồng quy tác dụng lên vật (lực đẩy, lực kéo, ma sát, lực cản…), ta có thể xác định được vector gia tốc a&x20D7;, từ đó mô tả và dự đoán chuyển động của vật.
• Tĩnh học vật rắn:
  • Xác định điều kiện cân bằng của một vật rắn chịu tác dụng của nhiều lực đồng quy. Điều kiện cân bằng là hợp lực của tất cả các lực tác dụng lên vật phải bằng không (F&x20D7;_{hợp lực} = 0).
• Y sinh cơ học và thể thao:
  • Phân tích lực tác dụng lên các khớp xương, cơ bắp của vận động viên khi thực hiện động tác (nhảy, chạy, ném…).
  • Thiết kế dụng cụ thể thao tối ưu (ví dụ: phân tích lực tác dụng lên vợt tennis, gậy golf).

Tóm lại, việc nắm vững cách xác định hợp lực của hai lực đồng quy là nền tảng không thể thiếu cho bất kỳ ai muốn nghiên cứu sâu hơn về cơ học, từ học sinh, sinh viên đến các kỹ sư, nhà vật lý trong công việc thực tế.

Câu hỏi thường gặp về hai lực đồng quy (FAQ)

Làm thế nào để xác định điểm đồng quy?

Điểm đồng quy là giao điểm của đường tác dụng (giá) của các lực. Nếu các lực có cùng điểm đặt trên vật, thì điểm đặt đó chính là điểm đồng quy. Nếu các lực có điểm đặt khác nhau, bạn cần kéo dài đường thẳng chứa vector của mỗi lực. Nếu các đường kéo dài này cắt nhau tại một điểm chung, đó chính là điểm đồng quy. Trong nhiều bài toán đơn giản hóa, ta thường coi các lực tác dụng lên vật là đồng quy tại trọng tâm của vật.

Hợp lực của hai lực đồng quy có thể bằng không không?

Có. Hợp lực của hai lực đồng quy bằng không khi và chỉ khi hai lực đó là hai lực cân bằng. Nghĩa là chúng phải cùng tác dụng lên một vật, có cùng độ lớn (F₁ = F₂), cùng phương, nhưng ngược chiều (α = 180°). Khi đó, áp dụng công thức tính độ lớn hợp lực: F = |F₁ – F₂| = 0.

Có thể tổng hợp nhiều hơn hai lực đồng quy không?

Có. Có nhiều cách để tổng hợp nhiều hơn hai lực đồng quy:

• Áp dụng quy tắc hình bình hành lặp lại: Tổng hợp hai lực đầu tiên (F&x20D7;₁, F&x20D7;₂) thành hợp lực F&x20D7;₁₂. Sau đó, tổng hợp F&x20D7;₁₂ với lực thứ ba (F&x20D7;₃) thành F&x20D7;₁₂₃, và cứ tiếp tục như vậy cho đến hết các lực.
• Sử dụng quy tắc đa giác lực: Vẽ lần lượt các vector lực nối đuôi nhau (ngọn vector trước là gốc vector sau). Vector hợp lực là vector nối từ gốc của vector đầu tiên đến ngọn của vector cuối cùng.
• Phương pháp chiếu: Chọn một hệ trục tọa độ vuông góc (Oxy). Chiếu tất cả các vector lực lên hai trục Ox và Oy. Tính tổng đại số các hình chiếu trên mỗi trục (F_x = ΣF_ix, F_y = ΣF_iy). Độ lớn hợp lực F được tính bằng F = √(F_x² + F_y²). Góc của hợp lực với trục Ox được tính bằng tan(θ) = F_y / F_x. Đây là phương pháp hiệu quả và chính xác, đặc biệt khi có nhiều lực.

Tổng hợp hai lực đồng quy

Công thức tính hợp lực có áp dụng cho mọi loại lực không?

Có. Công thức tính độ lớn hợp lực F2 = F12 + F22 + 2 * F1 * F2 * cos(α) và quy tắc hình bình hành áp dụng cho việc tổng hợp bất kỳ hai lực đồng quy nào, không phân biệt bản chất của chúng là lực cơ học (lực đẩy, kéo, ma sát, căng dây…), lực hấp dẫn, lực điện từ hay lực hạt nhân, miễn là chúng có thể được biểu diễn dưới dạng vector và có đường tác dụng cắt nhau tại một điểm.

Kết luận

Qua bài viết này, hy vọng bạn đã hiểu rõ hai lực đồng quy là gì – đó là hai lực có đường tác dụng cắt nhau tại một điểm. Việc xác định hợp lực của chúng, chủ yếu thông qua quy tắc hình bình hành và công thức tính độ lớn F² = F₁² + F₂² + 2 * F₁ * F₂ * cos(α), là một kỹ năng cơ bản nhưng vô cùng quan trọng trong Vật lý.