Hàm số liên tục là một phần kiến thức quan trọng trong chương trình Toán 11. Để làm được các bài tập về dạng này bạn cần nắm chắc lý thuyết và những tính chất cơ bản. Dưới đây Kiến thức THPT sẽ tổng hợp toàn bộ kiến thức và các dạng bài tập giúp bạn học tốt hơn. Hãy cùng theo dõi bài viết này nhé!
Hàm số liên tục là gì? Hàm số liên tục tại một điểm

Hàm số liên tục tại một điểm
Cho hàm số y = f(x) xác định trên K và x0 ∈ K.
– Hàm số y = f(x) liên tục tại x0 khi và chỉ khi ![]()
– Hàm số y = f(x) không liên tục tại x0 ta nói hàm số gián đoạn tại x0.
Hàm số liên tục trên một khoảng

Hàm số liên tục trên một khoảng
– Hàm số y = f(x) liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm x0 của khoảng đó.
– Hàm số y = f(x) liên tục trên [a; b] nếu nó liên tục trên (a; b) và ![]()
Các định lý cơ bản
Định lý 1:
– Hàm số đa thức liên tục trên toàn bộ tập .
– Các hàm số đa thức, phân thức hữu tỉ, lượng giác liên tục trên từng khoảng xác định của chúng.
Định lý 2: Cho các hàm số y = f(x) và y = g(x) liên tục tại x0. Khi đó:
– Các hàm số: y = f(x) + g(x); y = f(x) – g(x); y = f(x).g(x) liên tục tại x0.
– Hàm số ![]() liên tục tại x0 nếu g( x0 ) ≠ 0.
liên tục tại x0 nếu g( x0 ) ≠ 0.
Định lý 3: Cho hàm số y = f(x) liên tục trên [a; b] và f(a).f(b) < 0. Khi đó phương trình f(x) = 0 có ít nhất một nghiệm trên (a; b).
Một số dạng bài tập về hàm số liên tục Toán 11
Bài 1: Xét tính liên tục của các hàm số sau trên toàn trục số: f(x) = tan2x + cosx
Lời giải:
![]()
Bài 2: Xét tính liên tục của hàm số sau tại điểm chỉ ra
![]()
Lời giải:
Ta có:
![]()
Vậy hàm số liên tục tại x = 1
>> Xem thêm: Lý thuyết về Hàm số lượng giác chi tiết
Bài 3: Xét tính liên tục của hàm số sau tại điểm chỉ ra
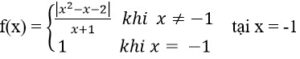
Lời giải:
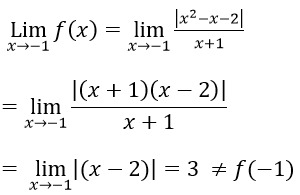
Vậy hàm số không liên tục tại điểm x = –1
Bài 4: Chọn giá trị f(0) để các hàm số sau liên tục tại điểm x = 0
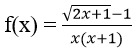
Lời giải:
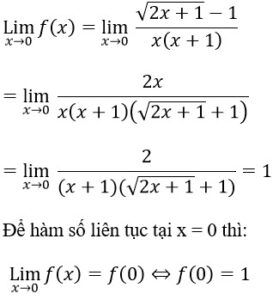
>> Xem thêm: Cấp số cộng là gì? Các dạng bài tập cơ bản
Bài 5: Xét tính liên tục của các hàm số sau tại điểm đã chỉ ra
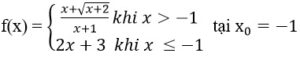
Lời giải:
Ta có:
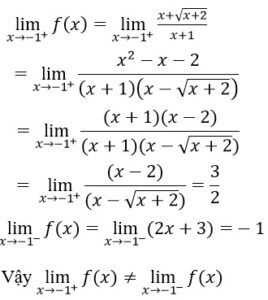
Vậy hàm số gián đoạn tại x = –1
Bài 6: Xác định a để hàm số sau liên tục trên R:
Hàm số xác định trên R
Với x < 2 ⇒ hàm số liên tục
Với x > 2 ⇒ hàm số liên tục
Với x = 2 ta có
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 2
Vậy a = -1, a = 0.5 là những giá trị cần tìm.


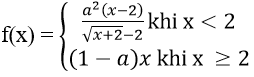
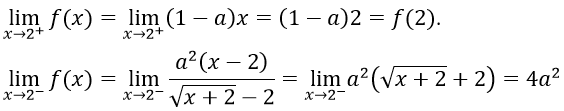
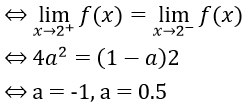









 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa