Hàm số lượng giác là kiến thức quan trọng trong chương trình Toán lớp 11 và được áp dụng rất nhiều trong tính toán. Vậy nên nắm chắc phần kiến thức rất quan trọng để có thể làm tốt những bài toán và đạt kết quả cao. Bài viết dưới đây Kiến Thức THPT sẽ giúp các em hiểu hơn về hàm số lượng giác để giải quyết phần bài tập này tốt hơn.
Định nghĩa hàm số lượng giác

– Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu là y = sinx.
Tập xác định của hàm số sin là ℝ.
– Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số côsin, kí hiệu là y = cosx.
Tập xác định của hàm số côsin là ℝ.
– Hàm số cho bằng công thức ( y = \sin{x} \cos{x} \) được gọi là hàm số tang, kí hiệu là y = tanx.
Tập xác định của hàm số tang là:
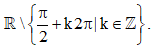
– Hàm số cho bằng công thức:
![]()
được gọi là hàm số côtang, kí hiệu là y = cotx.
Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Hàm số chẵn, hàm số lẻ
Cho hàm số y = f(x) có tập xác định là D.
– Hàm số f(x) được gọi là hàm số chẵn nếu ∀x ∈ D thì –x ∈ D thì f(–x) = f(x).
Đồ thị của một hàm số chẵn nhận trục tung là trục đối xứng.
– Hàm số f(x) được gọi là hàm số lẻ nếu ∀x ∈ D thì –x ∈ D thì f(–x) = – f(x).
Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
Nhận xét: Để vẽ đồ thị của một hàm số chẵn (tương ứng, lẻ), ta chỉ cần vẽ phần đồ thị của hàm số nằm ở bên phải trục tung, sau đó lấy đối xứng phần đồ thị đã vẽ qua trục tung (tương ứng, qua gốc tọa độ), ta sẽ được đồ thị của hàm số đã cho.
Ví dụ: Xét tính chẵn, lẻ của hàm số f(x) = x2 – 3.
Hướng dẫn giải
Tập xác định của hàm số f(x) là D = ℝ.
Do đó, nếu x ∈ D thì –x ∈ D.
Ta có: f(–x) = (–x)2 – 3 = x2 – 3 = f(x).
Vậy f(x) là hàm số chẵn.
>> Xem thêm >> Cấp số nhân – Lý thuyết toán 11 <<
Hàm số tuần hoàn
Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠ 0 sao cho với mọi x ∈ D ta có:
i) x + T ∈ D và x – T ∈ D;
ii) f(x + T) = f(x).
Số T dương nhỏ nhất thỏa mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần hoàn đó.
Nhận xét:
a) Các hàm số y = sinx và y = cosx tuần hoàn với chu kì 2ℼ. Các hàm số y = tanx và y = cotx tuần hoàn với chu kì ℼ.
b) Để vẽ đồ thị của một hàm số tuần hoàn với chu kì T, ta chỉ cần vẽ đồ thị của hàm số này trên đoạn [a; a + T], sau đó dịch chuyển song song với trục hoành phần đồ thị đã vẽ sang phải và sang trái các đoạn có độ dài lần lượt là T, 2T, 3T, … ta được toàn bộ đồ thị của hàm số.
Chú ý: Người ta chứng minh được các hàm số y = Asinωx và y = Acosωx (ω ≠ 0) là những hàm số tuần hoàn với chu kì T =.
Ví dụ: Xét tính tuần hoàn của hàm số y = cos2x.
Hướng dẫn giải
Hàm số có tập xác định là ℝ và với mọi số thực x, ta có:
x – ℼ ∈ ℝ, x + ℼ ∈ ℝ
cos2(x + ℼ) = cos (2x + 2ℼ) = cos2x
Vậy y = cos2x là hàm số tuần hoàn với chu kì T = ℼ.
>> Xem thêm >> Công thức tính cấp số cộng <<
Bài tập về tính chẵn lẻ của hàm số lượng giác
Bài tập 1. Xét tính chẵn, lẻ của các hàm số sau:
1) f(x) = sinx cosx;
2) g(x) = sin2x + cos2x.
Giải:
1) Tập xác định của hàm số f(x) là D = ℝ.
Do đó, nếu x ∈ D thì –x ∈ D.
do vậy, ta có f(–x) = sin(–x) cos(–x) = –sinx . cosx = – f(x).
Vậy hàm số f(x) = sinx cosx là hàm số lẻ.
2) Tập xác định của hàm số g(x) là D = ℝ.
Do đó, nếu x ∈ D thì –x ∈ D.
Ta có g(–x) = sin2(–x) + cos2(–x) = [–sinx]2 + cos(–2x) = sin2x + cos2x = f(x).
Vậy hàm số g(x) = sin2x + cos2x là hàm số chẵn.
Bài tập 2: Tìm tập nghiệm của phương trình: 3sin2x – 2√3 sinxcosx – 3cos2x = 0
Giải:
3sin2x – 2√3 sinxcosx – 3 cos2x=0 (1)
Xét cosx=0 (1) ⇔ sinx=0 (vô lý do: sin2x +cos2x=1)
Xét cosx ≠ 0. Chia cả hai vế của (1) cho cos2x. Ta được :
3tan2x-2√3 tanx-3=0
Bài tập 3: Tìm Nghiệm của phương trình 2(sinx + cosx) + sinxcosx = 2
Giải:
Đặt t = sinx + cosx. Đk: |t| ≤ √2. Khi đó
Ta có phương trình đã cho có dạng:
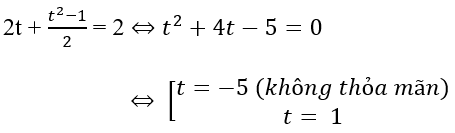
Trên đây là toàn bộ lý thuyết và bài tập hàm số lượng giác lớp 11 cơ bản. Để đạt kết quả cao ngoài việc tham khảo bài viết này, các em hãy thực hành thêm nhiều dạng bài khác nữa. Chúc các em học tốt và đạt kết quả cao trong các kỳ thi.


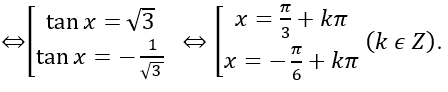
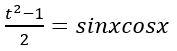
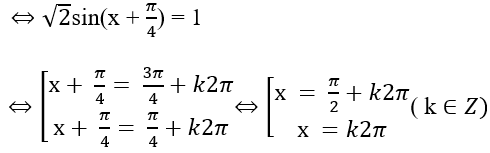









 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa