Lý thuyết Hệ trục tọa độ trong không gian Toán 12 (Chi tiết)

Bài viết Lý thuyết Hệ trục tọa độ trong không gian lớp 12 hay, chi tiết sẽ giúp các em nắm vững kiến thức trọng tâm Lý thuyết Hệ trục tọa độ trong không gian.

Hệ trục tọa độ trong không gian

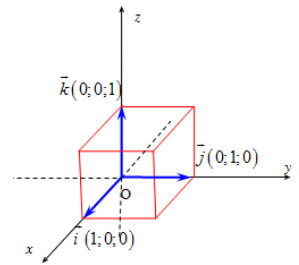
Trong không gian, xét ba trục toạ độ \( Ox \), \( Oy \), \( Oz \) vuông góc với nhau từng đôi một và chung một điểm gốc \( O \). Gọi \( \vec{i}, \vec{j}, \vec{k} \) là các vectơ đơn vị, tương ứng trên các trục \( Ox \), \( Oy \), \( Oz \). Hệ ba trục như vậy gọi là hệ trục toạ độ vuông góc trong không gian.

Chú ý: \( \vec{i}^2 = \vec{j}^2 = \vec{k}^2 = 1 \) và \( \vec{i} \cdot \vec{j} = \vec{i} \cdot \vec{k} = \vec{k} \cdot \vec{j} = 0 \).

Tọa độ của vectơ

Định nghĩa

\[
\vec{u} = (x; y; z) \iff \vec{u} = xi + yj + zk
\]

Tính chất

Cho \( \vec{a} = (a_1; a_2; a_3) \), \( \vec{b} = (b_1; b_2; b_3) \), \( k \in \mathbb{R} \)

\[
\vec{a} \pm \vec{b} = (a_1 \pm b_1; a_2 \pm b_2; a_3 \pm b_3)
\]

\[
k\vec{a} = (ka_1; ka_2; ka_3)
\]

\[
\vec{a} = \vec{b} \iff \begin{cases}
a_1 = b_1 \\
a_2 = b_2 \\
a_3 = b_3
\end{cases}
\]

\[
\vec{0} = (0; 0; 0), \vec{i} = (1; 0; 0), \vec{j} = (0; 1; 0), \vec{k} = (0; 0; 1)
\]

\(\vec{a}\) cùng phương \(\vec{b}\) (\(\vec{b} \neq \vec{0}\)) \( \iff \vec{a} = k \vec{b}\) (k là hằng số thực)

\[
\vec{a} = k \vec{b} \iff \begin{cases}
a_1 = kb_1 \\
a_2 = kb_2 \\
a_3 = kb_3
\end{cases}
\iff \frac{a_1}{b_1} = \frac{a_2}{b_2} = \frac{a_3}{b_3} \quad (b_1, b_2, b_3 \neq 0)
\]

\[
\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3
\]

\(\vec{a} \perp \vec{b} \iff a_1b_1 + a_2b_2 + a_3b_3 = 0\)

\[
\vec{a}^2 = a_1^2 + a_2^2 + a_3^2
\]

\[
|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}
\]

\[
\cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} = \frac{a_1b_1 + a_2b_2 + a_3b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2} \sqrt{b_1^2 + b_2^2 + b_3^2}} \quad (\text{với } \vec{a}, \vec{b} \neq \vec{0})
\]

Xem thêm:

• Đường tiệm cận của đồ thị hàm số
• Phương trình mặt cầu

Bài tập về hệ trục tọa độ trong không gian

Bài 1: Cho đường thẳng và mặt cầu \( (S): x^2 + y^2 + z^2 – 2x + 4z + 1 = 0 \). Số điểm chung của \( \Delta \) và \( S \) là:

\[
\text{A. } 0 \quad \text{B. } 1 \quad \text{C. } 2 \quad \text{D. } 3
\]

Lời giải:

Đường thẳng \( \Delta \) đi qua \( M(0; 1; 2) \) và có một vectơ chỉ phương là \( \vec{u} = (2; 1; -1) \).

Mặt cầu \( (S) \) có tâm \( I(1; 0; -2) \) và bán kính \( R = 2 \).

Ta có \( \overrightarrow{MI} = (1; -1; -4) \) và \( [\vec{u}, \overrightarrow{MI}] = (-5; 7; -3) \), do đó:

\[
\text{Vì } d(I, \Delta) > R \text{ nên } \Delta \text{ không cắt mặt cầu } (S).
\]

Bài 2: Cho điểm \( I(1; -2; 3) \). Phương trình mặt cầu tâm \( I \) và tiếp xúc với trục \( Oy \) là:

\[
\text{A. } (x – 1)^2 + (y + 2)^2 + (z – 3)^2 = \sqrt{10}
\]
\[
\text{B. } (x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 10
\]
\[
\text{C. } (x + 1)^2 + (y^2 + 2)^2 + (z + 3)^2 = 10
\]
\[
\text{D. } (x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 9
\]

Lời giải

Gọi \( M \) là hình chiếu của \( I(1; -2; 3) \) lên \( Oy \), ta có \( M(0; -2; 0) \).

Tính \( \overrightarrow{IM} = (-1; 0; -3) \), do đó bán kính \( R = d(I, Oy) = IM = \sqrt{10} \) là bán kính của mặt cầu cần tìm.

Phương trình mặt cầu là:

\[
(x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 10
\]