Trong bộ câu hỏi thi THPTQG, phần toán 12 nguyên hàm luôn chiếm tỷ lệ đáng kể. Vì vậy, các sĩ tử từ cần tập trung ôn luyện phần kiến thức này ngay từ bây giờ để nâng cao kỹ năng và thành thạo giải các bài toán liên quan. Kiến Thức THPT sẽ tổng hợp đầy đủ lý thuyết về nguyên hàm và hướng dẫn các em “thực chiến” các dạng toán thường xuất hiện trong đề thi ngay dưới đây!
Nguyên hàm và tính chất

Nguyên hàm
– Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
– Định lí:
- Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C
Tính chất của nguyên hàm
– Tính chất 1: (∫f(x)dx)’ = f(x) và ∫f'(x)dx = f(x) + C
– Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
– Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
Bảng nguyên hàm cơ bản của một số hàm số thường gặp

>> Xem thêm: Tính đơn điệu của hàm số
Phương pháp tính nguyên hàm

Phương pháp đổi biến số
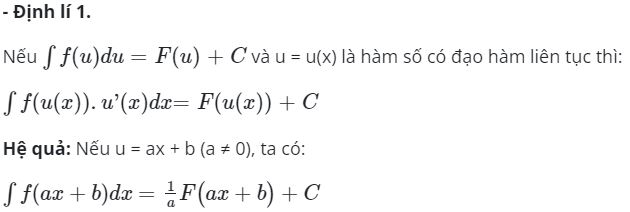
>> Xem thêm: Xác suất có điều kiện
Phương pháp nguyên hàm từng phần
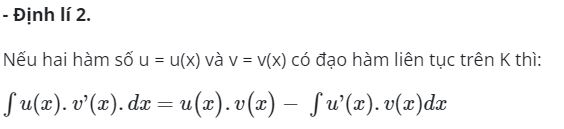
Bài tập về công thức nguyên hàm
Bài 1: Tính
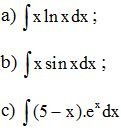
Lời giải:
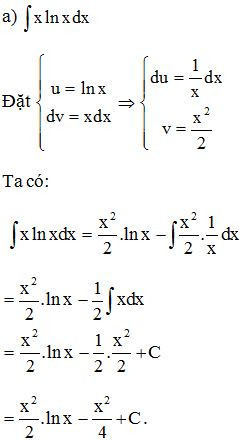
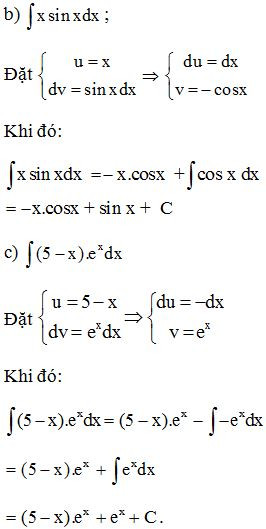
Trên đây là toàn bộ kiến thức về nguyên hàm cũng như một số dạng bài tập thường gặp mà chúng tôi đã chọn lọc và tổng hợp. Hy vọng bài viết trên sẽ hữu ích và giúp các bạn nắm chắc kiến thức để từ đó có thể áp dụng thành thạo vào các bài tập. Chúc các bạn học tốt!!!











 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa