Khái niệm phương trình tương đương
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x)=0 tương đương với phương trình g(x)=0 thì ta viết
f(x)=0⇔g(x)=0
Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
Phương trình sin x = m
Phương trình sinx=m có nghiệm khi và chỉ khi |m|≤1.
Khi |m|≤1 sẽ tồn tại duy nhất α∈[−π2;π2] thoả mãn sinα=m. Khi đó:
sinx=m⇔sinx=sinα⇔{x=α+k2πx=π–α+k2π(k∈Z)
Chú ý:
– Nếu số đo của góc α được cho bằng đơn vị độ thì
sinx=sinα∘⇔{x=α∘+k360∘x=180∘–α∘+k360∘(k∈Z)
– Một số trường hợp đặc biệt:
sinx=0⇔x=kπ,k∈Z.
sinx=1⇔x=π2+k2π,k∈Z.
sinx=−1⇔x=−π2+k2π,k∈Z.
Phương trình cos x = m
– Phương trình cosx=m có nghiệm khi và chỉ khi |m|≤1.
– Khi |m|≤1 sẽ tồn tại duy nhất α∈[0;π] thoả mãn cosα=m. Khi đó:
cosx=m⇔cosx=cosα⇔{x=α+k2πx=−α+k2π(k∈Z)
Chú ý:
– Nếu số đo của góc α được cho bằng đơn vị độ thì
cosx=cosα∘⇔{x=α∘+k360∘x=−α∘+k360∘(k∈Z)
– Một số trường hợp đặc biệt:
cosx=0⇔x=π2+kπ,k∈Z.
cosx=1⇔x=k2π,k∈Z.
cosx=−1⇔x=π+k2π,k∈Z.
>> Xem thêm: Hàm số liên tục là gì?
Phương trình tan x = m
Phương trình tan x = m có nghiệm với mọi m.
Với mọi m∈R, tồn tại duy nhất α∈(−π2;π2) thoả mãn tanα=m. Khi đó:
tanx=m⇔tanx=tanα⇔x=α+kπ,k∈Z.
Chú ý: Nếu số đo của góc α được cho bằng đơn vị độ thì
tanx=tanα∘⇔x=α∘+k180∘,k∈Z.
Phương trình cot x = m
Phương trình cot x = m có nghiệm với mọi m.
Với mọi m∈R, tồn tại duy nhất α∈(0;π) thoả mãn cotα=m. Khi đó:
cotx=m⇔cotx=cotα⇔x=α+kπ,k∈Z.
Chú ý: Nếu số đo của góc α được cho bằng đơn vị độ thì
cotx=cotα∘⇔x=α∘+k180∘,k∈Z.
>> Xem thêm: Phép chiếu song song
Sử dụng máy tính cầm tay tìm góc khi biết giá trị lượng giác của nó
Bước 1: Chọn đơn vị đo góc (độ hoặc radian)
Muốn tìm số đo độ, ta ấn: SHIFT→MODE→3 (CASIO FX 570VN).
Muốn tìm số đo radian, ta ấn: SHIFT→MODE→4 (CASIO FX 570VN).
Bước 2: Tìm số đo góc
Khi biết sin,cos,tan của góc α ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím sin,cos,tan rồi nhập giá trị lượng giác m và cuối cùng ấn phím “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc α.
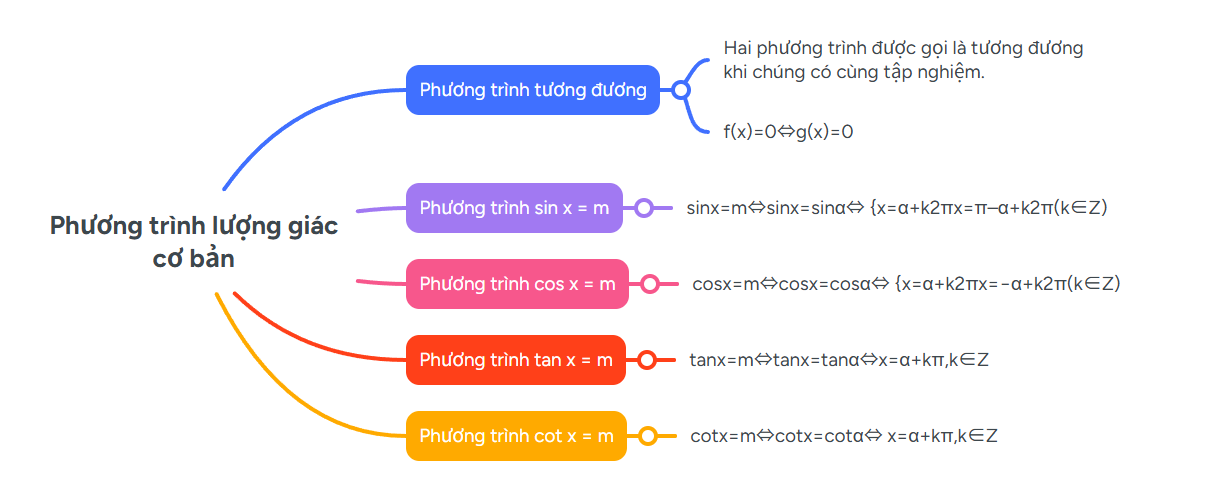
Chốt lại ta có sơ đồ tư duy phương trình lượng giác cơ bản như sau:










 Giới thiệu
Giới thiệu Chính sách bảo mật
Chính sách bảo mật Câu hỏi thường gặp
Câu hỏi thường gặp Liên hệ
Liên hệ Kiến thức lớp 10
Kiến thức lớp 10 Cẩm nang học tập
Cẩm nang học tập Định nghĩa
Định nghĩa