Lý thuyết Bài 14: Phương trình mặt phẳng lớp 12 tập 2 KNTT

Phương trình mặt phẳng lớp 12 là một phần quan trọng trong chương trình toán học, giúp học sinh nắm vững kiến thức về hình học không gian. Hãy cùng khám phá để hiểu rõ hơn về khái niệm này.

Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng

Khái niệm vectơ pháp tuyến – phương trình mặt phẳng lớp 12

Vectơ \(\vec{n} \neq \vec{0}\) được gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của \(\vec{n}\) vuông góc với (α).

Chú ý:

Mặt phẳng hoàn toàn xác định khi biết một điểm và một vectơ pháp tuyến của nó

Nếu \(\vec{n}\) là một vectơ pháp tuyến của mặt phẳng (α) thì \(k \vec{n}\) (với k là một số khác 0) cũng là một vectơ pháp tuyến của (α).

Ví dụ 1 . Cho hình chóp đều S.ABCD. Tìm một vectơ pháp tuyến của mặt phẳng (ABCD).

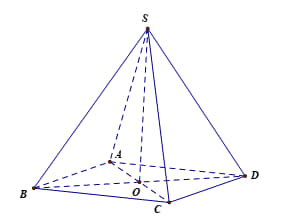
Hình chóp đều S.ABCD

Bài giải: 

Gọi O là giao điểm của AC và BD.

Vì S.ABCD là hình chóp đều nên SO ^ (ABCD).

Do đó \(\overrightarrow{SO}\) là một vectơ pháp tuyến của mặt phẳng (ABCD).

Cách tìm một vectơ vuông góc với hai vectơ cho trước

Trong không gian Oxyz, cho hai vectơ \(\vec{u} = (a; b; c) \quad \text{và} \quad \vec{v} = (a’; b’; c’)\). Khi đó vectơ \(\vec{n} = (b c’ – b’ c; \, c a’ – c’ a; \, a b’ – a’ b)\) vuông góc với cả hai vectơ \(\vec{n}\) và \(\vec{v}\), được gọi là tích có hướng của \(\vec{n}\) và \(\vec{v}\), kí hiệu là [\(\vec{n}\); \(\vec{v}\)]

Ví dụ 2. Trong không gian Oxyz, cho \(\vec{u}\) = (1; 2; 3) và \(\vec{v}\) = (0; -1; 2). Tìm  [\(\vec{u}\); \(\vec{v}\)].

Bài giải:

\(\text{Ta có } [\vec{u}, \vec{v}] = \left( \left| \begin{array}{cc} 2 & 3 \\ -1 & 2 \end{array} \right|; \, \left| \begin{array}{cc} 3 & 1 \\ 2 & 0 \end{array} \right|; \, \left| \begin{array}{cc} 1 & 2 \\ 0 & -1 \end{array} \right| \right) = (7; -2; -1)\)

Khái niệm cặp vectơ chỉ phương của mặt phẳng

Trong không gian Oxyz, hai vectơ \(\vec{n}\) và \(\vec{v}\) được gọi là cặp vectơ chỉ phương của mặt phẳng (P) nếu chúng không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).

Nếu \(\vec{n}\) và \(\vec{v}\) là cặp vectơ chỉ phương của (P) thì \( [\vec{u}, \vec{v}]\) là một vectơ pháp tuyến của (P).

Ví dụ 3. Trong không gian Oxyz, cho các vectơ \(\vec{u} = (0; -1; 3) \quad \text{và} \quad \vec{v} = (5; 0; 1)\). Gọi (P) là một mặt phẳng song song với các giá của . Hãy tìm một vectơ pháp tuyến của (P).

Bài giải:

Ta có \(\vec{n} = [\vec{u}, \vec{v}] = \left( \left| \begin{array}{cc} -1 & 3 \\ 0 & 1 \end{array} \right|; \, \left| \begin{array}{cc} 3 & 0 \\ 1 & 5 \end{array} \right|; \, \left| \begin{array}{cc} 0 & -1 \\ 5 & 0 \end{array} \right| \right) = (-1; 15; 5)\) là một vectơ pháp tuyến của mặt phẳng (P).

Phương trình tổng quát của mặt phẳng

Khái niệm phương trình tổng quát của mặt phẳng

Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó.

Ví dụ 4. Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x + y – z + 5 = 0. Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (P).

Bài giải:

Mặt phẳng (P) nhận \(\vec{n} = (2; 1; -1)\) làm một vectơ pháp tuyến.

Tổng quát phương trình mặt phẳng lớp 12

Lập phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến

Trong không gian Oxyz, nếu mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và có vectơ pháp tuyến \(\vec{n} = (A; B; C) \\) thì có phương trình là:

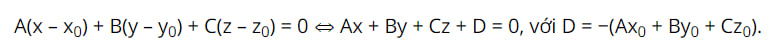
Phương trình vectơ pháp tuyến

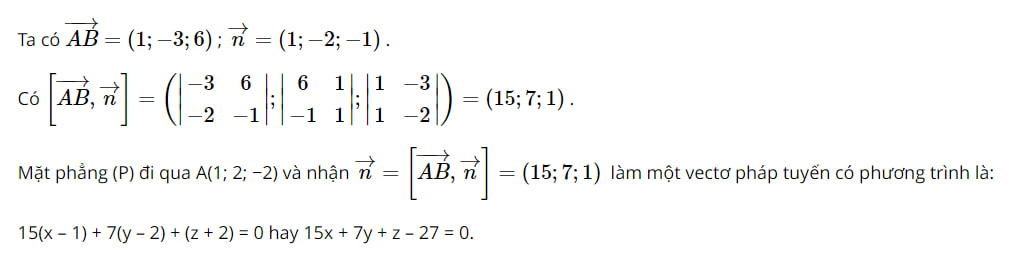
Phương trình mặt phẳng

Ví dụ 5. Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua A(0; 2; 3) và có vectơ pháp tuyến \(\vec{n} = (2; 1; -1)\)

Bài giải:

Mặt phẳng (P) có phương trình là:

2(x – 0) + 1(y – 2) – 1(z – 3) = 0 Û 2x + y – z + 1 = 0.

Lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\vec{u}, \vec{v}\) có thể thực hiện theo các bước sau:

Tìm vectơ pháp tuyến \(\vec{n} = [\vec{u}, \vec{v}]\)

Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến \(\vec{n}\)

Ví dụ 6. Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua A(1; 2; −2), B(2; −1; 4) và song song với giá của vectơ \(\vec{n}\) = (1;  −2;  −1).

Bài giải:

Lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:

Tìm cặp vectơ chỉ phương \(\vec{AB}, \vec{AC}\)

Tìm vectơ pháp tuyến \(\vec{n} = [\vec{AB}, \vec{AC}]\)

Lập phương trình tổng quát của mặt phẳng đi qua A và có vectơ pháp tuyến\( \vec{n}\).

Ví dụ 7. Trong không gian Oxyz, viết phương trình mặt phẳng đi qua ba điểm A(1; 0; −2), B(1; 1; 1), C(0; −1; 2).

Bài giải:

Phương trình mặt phẳng đi qua ba điểm

Điều kiện để hai mặt phẳng vuông góc với nhau

Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A’x + B’y + C’z + D’ = 0 với hai vectơ pháp tuyến \(\vec{n} = (A; B; C), \quad \vec{n}’ = (A’; B’; C’)\) tương ứng. Khi đó: (α) ⊥ (β) \(\Leftrightarrow \vec{n} \perp \vec{n}’ \Leftrightarrow AA’ + BB’ + CC’ = 0\)

Ví dụ 8. Trong không gian Oxyz, cho mặt phẳng (P): x + 2y + z + 1 = 0 và mặt phẳng (Q): 3x – 2y + z + 5 = 0. Chứng minh rằng hai mặt phẳng (P) và (Q) vuông góc với nhau.

Bài giải

\(\text{Ta có } \vec{n}_P = (1; 2; 1), \quad \vec{n}_Q = (3; -2; 1). \text{Vì } \vec{n}_P \cdot \vec{n}_Q = 1 \cdot 3 + 2 \cdot (-2) + 1 \cdot 1 = 0. \text{ Do đó } (P) \perp (Q).\)

Điều kiện để hai mặt phẳng song song với nhau

Trong không gian Oxyz, cho hai mặt phẳng (α): Ax + By + Cz + D = 0, (β): A’x + B’y + C’z + D’ = 0, với các vectơ pháp tuyến

\(\vec{n} = (A; B; C), \quad \vec{n}’ = (A’; B’; C’) \text{ tương ứng. Khi đó: } (\alpha) \parallel (\beta) \Leftrightarrow \begin{cases} \vec{n}’ = k \vec{n} \\ D’ \neq k D \quad \text{với một } k \text{ nào đó.} \end{cases}\)

Chú ý:

Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.

Hai mặt phẳng (α) và (β) trùng nhau khi và chỉ khi tồn tại số k khác 0 sao cho A’ = kA, B’ = kB, C’ = kC, D’ = kD.

Ví dụ 9. Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(0; 1; 3) và song song với mặt phẳng (Q): 2x – 3z + 1 = 0.

Bài giải:

Có \(\vec{n}_Q = (2; 0; -3)\) là vectơ pháp tuyến của mặt phẳng (Q).

Vì (P) // (Q) nên mặt phẳng (P) nhận \(\vec{n} = \vec{n}_Q = (2; 0; -3)\) làm một vectơ pháp tuyến.

Mặt phẳng (P) đi qua điểm M(0; 1; 3), có \(\vec{n} = (2; 0; -3)\) là vectơ pháp tuyến có phương trình là: 2x – 3(z – 3) = 0 hay 2x – 3z + 9 = 0.

Khoảng cách từ một điểm đến một mặt phẳng

Trong không gian Oxyz, khoảng cách từ điểm M(x0; y0; z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 là \(d(M, (P)) = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}\)

Ví dụ 10. Trong không gian Oxyz, tính khoảng cách từ điểm I(−1; 2; 1) đến mặt phẳng (α): x + 2y – 2z + 8 = 0.

Bài giải:

\(\text{Ta có } d(I, (\alpha)) = \frac{|-1 + 2 \cdot 2 – 2 \cdot 1 + 8|}{\sqrt{1^2 + 2^2 + (-2)^2}} = \frac{9}{3} = 3.\)

Bài viết đã nêu ra được hết lý thuyết, công thức phương trình mặt phẳng cùng với các phần ví dụ chi tiết, ngắn gọn nhất. Hy vọng các Kiến thức trong bài sẽ giúp các em giải các phần bài tập khác tốt hơn

<<Xem thêm>> Lý thuyết ứng dụng hình học của tích phân Toán 12