Lý thuyết, bài tập về tính đơn điệu của hàm số lớp 12

Tóm tắt lý thuyết Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số sách Kết nối tri thức hay, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Tính đơn điệu của hàm số

Tính đồng biến, nghịch biến của hàm số

Giả sử K là khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là hàm số xác định trên K.

– Hàm số y = f(x) gọi là đồng biến trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒  f(x1) < f(x2).

– Hàm số y = f(x) gọi là nghịch biến trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).

Chú ý:

– Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải (H.1.3a).

– Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (H.1.3b).

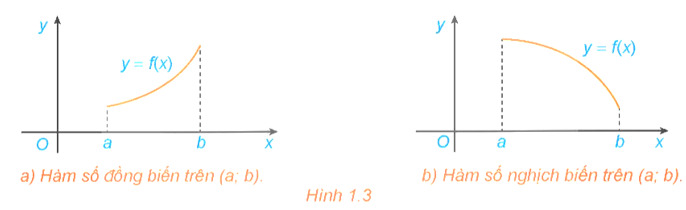
– Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

– Khi xét tính đơn điệu của hàm số mà không chỉ rõ tập K thì ta hiểu là xét trên tập xác định của hàm số đó.

Tính đơn điệu và dấu của đạo hàm

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

– Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên khoảng K.

– Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên khoảng K.

Chú ý:

– Định lí trên vẫn đúng trong trường hợp f'(x) bằng 0 tại một số hữu hạn điểm trong khoảng K.

– Người ta chứng minh được rằng, nếu f'(x) = 0 với mọi x ∈ K thì hàm số f(x) không đổi trên khoảng K.

Cực trị của hàm số

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (a có thể là −∞, b có thể là +∞) và điểm x0 ∈ (a; b).

– Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x ∈ (x0 – h; x0 + h) ⊂ (a; b) và x ≠ x0 thì ta nói hàm số f(x) đạt cực đại tại x0.

– Nếu tồn tại h > 0 sao cho f(x) > f(x0) với mọi x ∈ (x0 – h; x0 + h) ⊂ (a; b) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.

Chú ý:

– Nếu hàm số y = f(x) đạt cực đại tại x0 thì x0 được gọi là điểm cực đại của hàm số f(x). Khi đó, f(x0) được gọi là giá trị cực đại của hàm số f(x) và kí hiệu fCĐ hay yCĐ. Điểm M0(x0; f(x0)) được gọi là điểm cực đại của đồ thị hàm số.

– Nếu hàm số y = f(x) đạt cực tiểu tại x0 thì x0 được gọi là điểm cực tiểu của hàm số f(x). Khi đó, f(x0) được gọi là giá trị cực tiểu của hàm số f(x) và kí hiệu là  fCĐ hay yCĐ. Điểm M0(x0; f(x0)) được gọi điểm cực tiểu của đồ thị hàm số.

– Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) của hàm số.

Mối liên hệ giữa đạo hàm và cực trị

Giả sử hàm số y = f(x) liên tục trên khoảng (a; b) chứa điểm x0 và có đạo hàm trên các khoảng (a; x0) và (x0; b). Khi đó

– Nếu f‘(x) < 0 với mọi x ∈ (a; x0) và f‘(x) > 0 với mọi x ∈ (x0; b) thì x0 là một điểm cực tiểu của hàm số f(x).

– Nếu f‘(x) > 0 với mọi x ∈ (a; x0) và f‘(x) < 0 với mọi x ∈ (x0; b) thì x0 là một điểm cực đại của hàm số f(x).

Các bước tìm điểm cực trị của hàm số f(x)

Bước 1. Tìm tập xác định của hàm số f(x):

Bước 2. Tính đạo hàm f‘(x). Tìm các điểm mà tại đó đạo hàm f'(x) bằng 0 hoặc đạo hàm không tồn tại.

Bước 3. Lập bảng biến thiên của hàm số.

Bước 4.Từ bảng biến thiên suy ra các cực trị của hàm số.

Bài tập về tính đơn điệu của hàm số

Bài tập 1: Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy tìm các khoảng đồng biến, nghịch biến của hàm số.

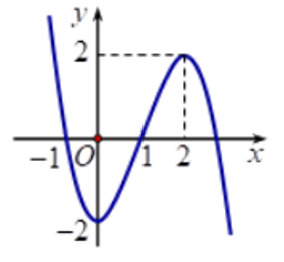
Lời giải:

Từ đồ thị hàm số, ta có:

– Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).

– Hàm số đồng biến trên khoảng (0; 2).

Bài tập 2: Cho hàm số có đồ thị như hình vẽ. Hãy tìm các cực trị của hàm số.

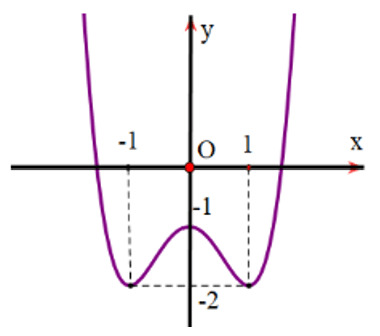
Lời giải:

Từ đồ thị hàm số, ta có:

Hàm số đạt cực tiểu tại x = −1 và yCT = y(−1) = −2.

Hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = −1.

Hàm số đạt cực tiểu tại x = 1 và yCT = y(1) = −2.

Bài 3: Cho hàm số y = f(x) có bảng biến thiên như sau:

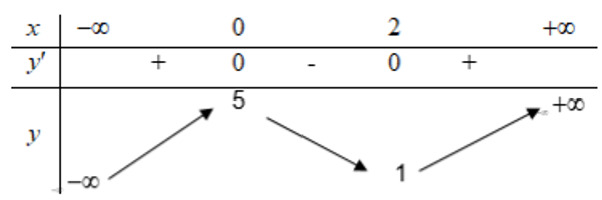
Tìm cực trị của hàm số trên.

Lời giải:

Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực đại tại x = 0 và yCĐ  = y(0) = 5.

Hàm số đạt cực tiểu tại x = 2 và yCT = y(2) = 1.

Xem thêm bộ bài tập trắc nghiệm chuyên đề tính đơn điệu hàm số tại:

Trên đây là toàn bộ kiến thức về tính đơn điệu của hàm số cũng như một số dạng bài tập thường gặp mà kienthucthpt đã tổng hợp. Hy vọng bài viết trên sẽ hữu ích và giúp các bạn nắm chắc kiến thức tính đơn điệu của hàm số để từ đó có thể áp dụng thành thạo vào các bài tập. Chúc các bạn học tốt!!!