Tổng hợp lực là gì? Công thức tổng hợp lực – Vật lý 10

Tổng hợp lực – Hợp lực tác dụng

– Tổng hợp lực là gì? Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy.

– Lực thay thế này gọi là hợp lực.

– Biểu thức:
\[
\vec{F} = \vec{F_1} + \vec{F_2} + \vec{F_3} + \dots
\]

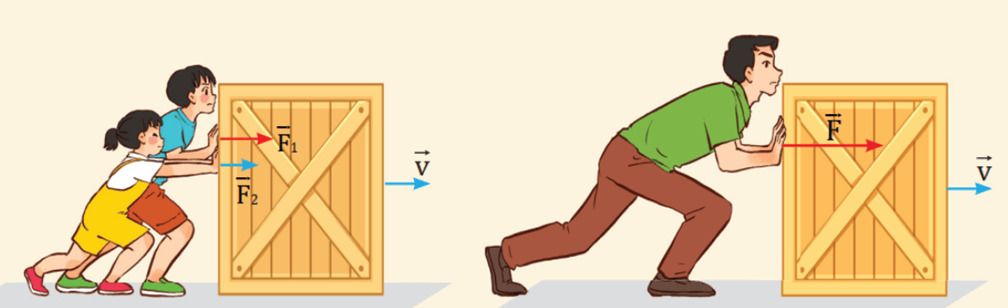
Lực \(\vec{F}\) được coi là hợp lực của lực \(\vec{F_1}\) và \(\vec{F_2}\).

Tổng hợp hai lực cùng phương

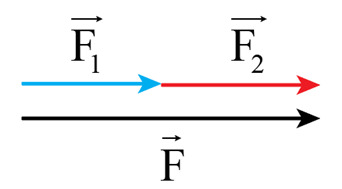
– Hai lực cùng phương, cùng chiều thì làm tăng tác dụng lên vật và có độ lớn hợp lực bằng:
\[
F = F_1 + F_2
\]

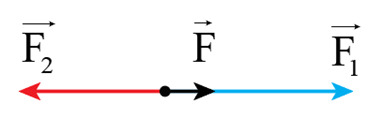
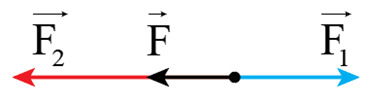
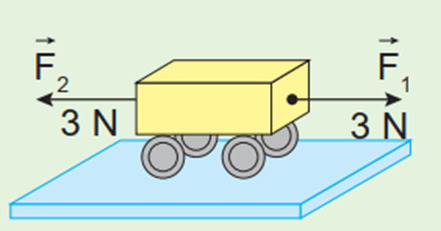
– Hai lực cùng phương, ngược chiều thì chúng hạn chế, thậm chí có thể triệt tiêu tác dụng của nhau lên vật và hợp lực có giá trị bằng:
\[
F = F_1 – F_2
\]
+ Nếu \(F > 0\) thì hợp lực \(F\) cùng chiều với lực thành phần \(F_1\).

+ Nếu \(F < 0\) thì lực \(F\) ngược chiều với lực \(F_1\).

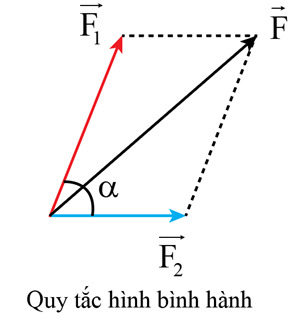
Tổng hợp hai lực đồng quy – Quy tắc hình bình hành

– Bước 1: Vẽ hai vectơ \(\vec{F_1}\) và \(\vec{F_2}\) đồng quy tại \(O\).

– Bước 2: Vẽ một hình bình hành có hai cạnh liền kề trùng với hai vectơ \(\vec{F_1}\) và \(\vec{F_2}\).

– Bước 3: Vẽ đường chéo của hình bình hành có cùng gốc \(O\). Vectơ hợp lực \(\vec{F}\) trùng với đường chéo này.

>> Xem thêm: Chuyển động thẳng biến đổi đều

Các lực cân bằng và không cân bằng

Các lực cân bằng

Vật đứng yên dưới tác dụng của nhiều lực, khi đó tổng hợp các lực tác dụng lên vật bằng 0. Ta nói các lực tác dụng lên vật là các lực cân bằng và vật ở trạng thái cân bằng.
\[
\vec{F} = \vec{F_1} + \vec{F_2} + \vec{F_3} + \dots = 0
\]

Các lực không cân bằng

Khi hợp lực của các lực khác 0 thì các lực này không cân bằng. Hợp lực hay các lực không cân bằng này tác dụng vào một vật có thể làm thay đổi vận tốc của vật.

Phân tích lực

Phân tích lực là phép thay thế một lực thành hai lực thành phần có tác dụng giống hệt như lực ấy.

Quy tắc

Người ta thường phân tích lực thành hai lực thành phần vuông góc với nhau để lực thành phần này không có tác dụng nào theo phương của lực thành phần kia.

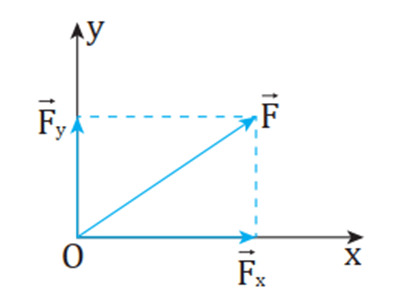
Phân tích lực \(\vec{F}\) thành hai thành phần vuông góc là \(\vec{F_x}; \vec{F_y}\).

>> Xem thêm: Chuyển động ném

Chú ý

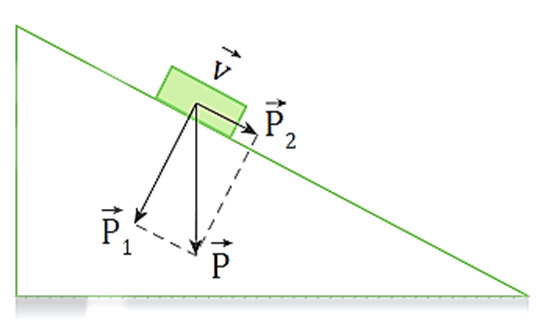
– Chỉ khi xác định được một lực có tác dụng theo hai phương vuông góc nào thì mới phân tích lực theo hai phương vuông góc đó.

– Ví dụ: vật trượt xuống dưới trên mặt phẳng nghiêng, trọng lực \(\vec{P}\) được phân tích thành hai lực thành phần \(\vec{P_1}; \vec{P_2}\) vì xác định được trọng lực có tác dụng ép vật vào mặt phẳng nghiêng và kéo vật trượt xuống dưới.

Một số dạng bài tập tổng hợp lực